Предмет: Алгебра,
автор: ivanmerkusev74
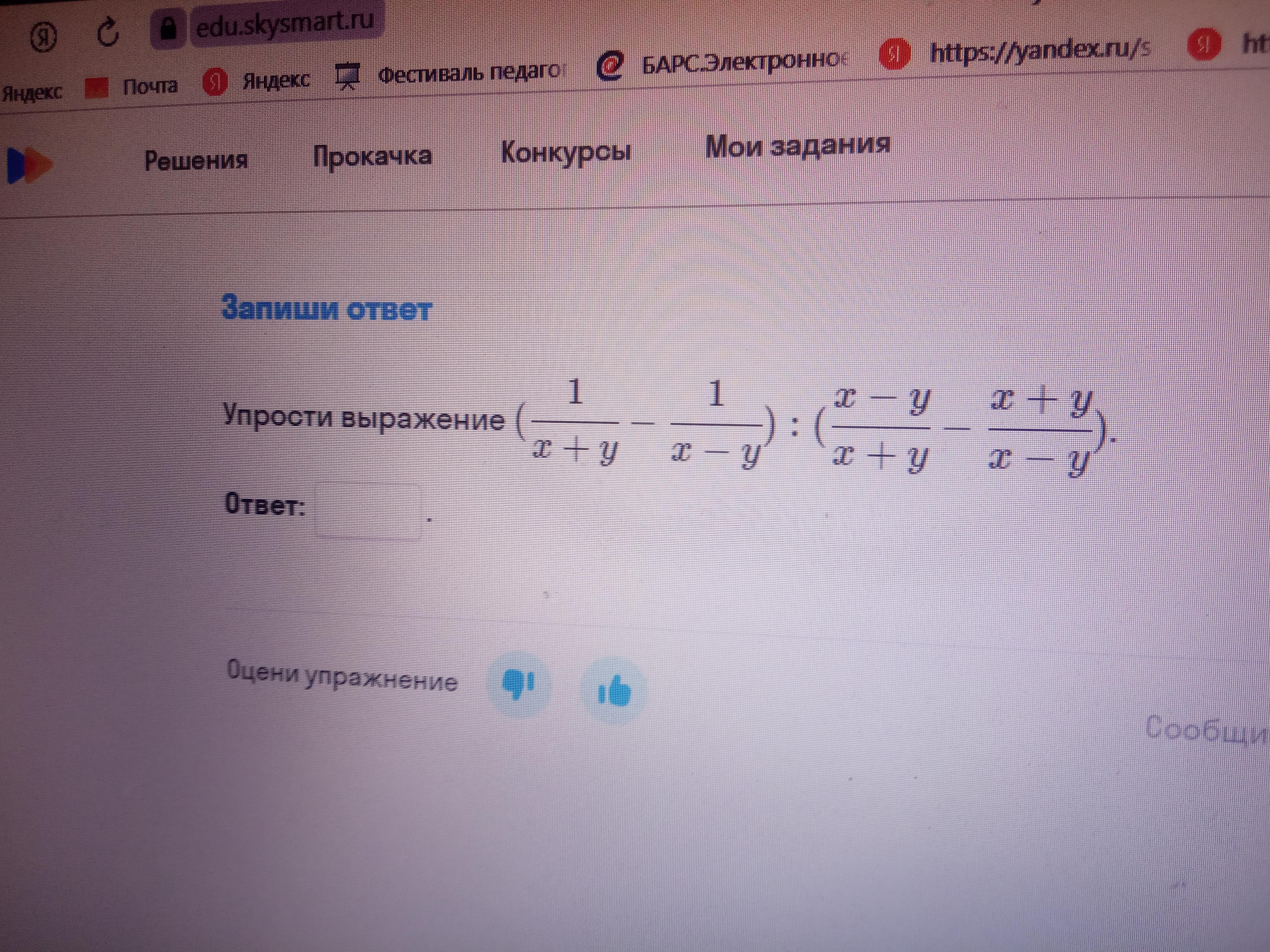
Можно пожалуйста поьыстрей
Приложения:
Ответы
Автор ответа:
0
При решении использованы формулы разности квадратов, квадрата суммы и квадрата разности:
Похожие вопросы
Предмет: Окружающий мир,
автор: KiselevVM
Предмет: Русский язык,
автор: Lady220
Предмет: Окружающий мир,
автор: KittyCheshir1
Предмет: Алгебра,
автор: Flammen
Предмет: Литература,
автор: jjjo440