Предмет: Математика,
автор: jarkoi0912
помогите решить дам 50 баллов
Приложения:
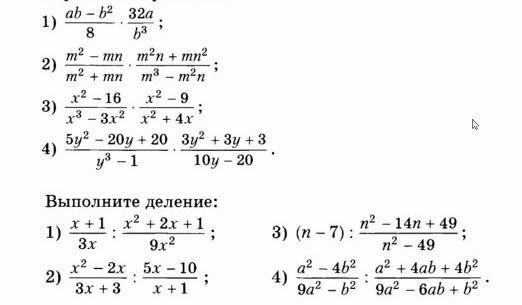
Ответы
Автор ответа:
0
1)
2)
3)
4)
1)
2)
3)
4)
Похожие вопросы
Предмет: Русский язык,
автор: SashaNeych
Предмет: Русский язык,
автор: Вероника252
Предмет: Русский язык,
автор: Катя11118
Предмет: Математика,
автор: thomas1833
Предмет: Математика,
автор: yugu