Предмет: Геометрия,
автор: sleinaveronika881
Начертите в тетради свой вектор на координатной плоскости и найдите для него координаты с ередины отрезка, длину вектор а и расстояние между двумя точками?
Ответы
Автор ответа:
0
Объяснение:
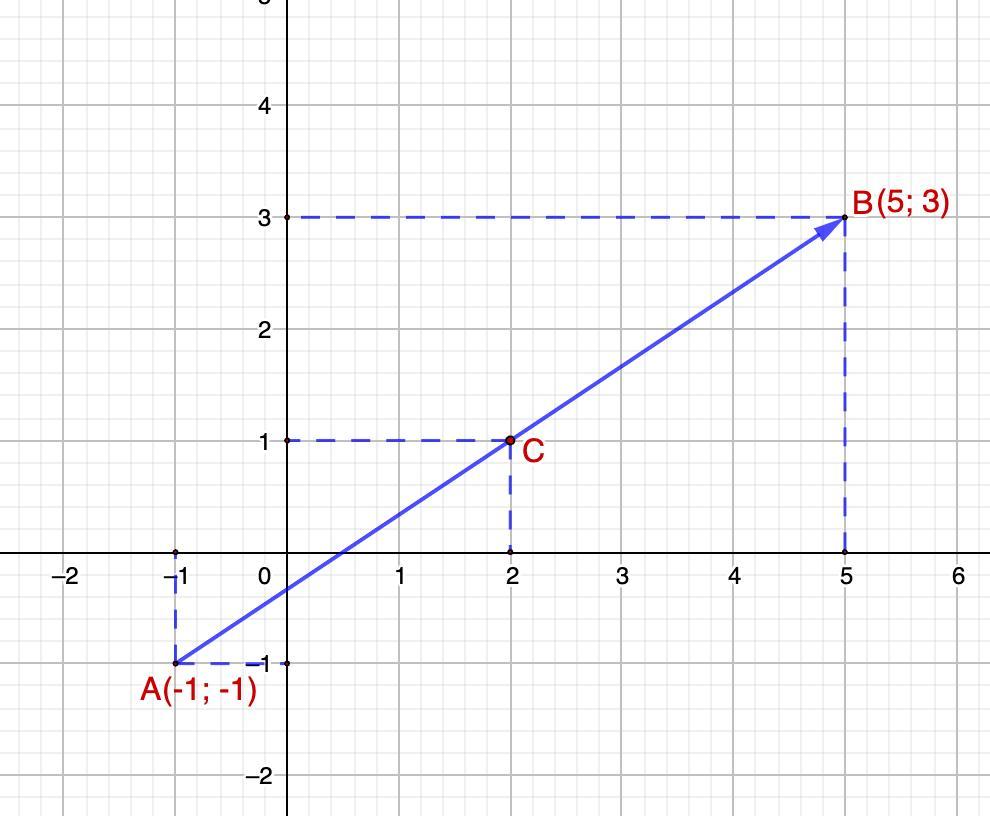
На координатной плоскости отметим две точки А и В.
Координаты точки А (-1; -1), точки В (5; 3)
Проведем вектор .
Найдем координаты вектора :
Длина вектора:
Найдем координаты середины отрезка С:
То есть С(2; 1)
Расстояние между двумя точками:
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: sashanuraev
Предмет: Английский язык,
автор: azaliya071
Предмет: Русский язык,
автор: sanekistra
Предмет: Математика,
автор: alya7965
Предмет: Биология,
автор: eppochh