Предмет: Алгебра,
автор: school88oren
Помогите решить каким способом не важно
Приложения:
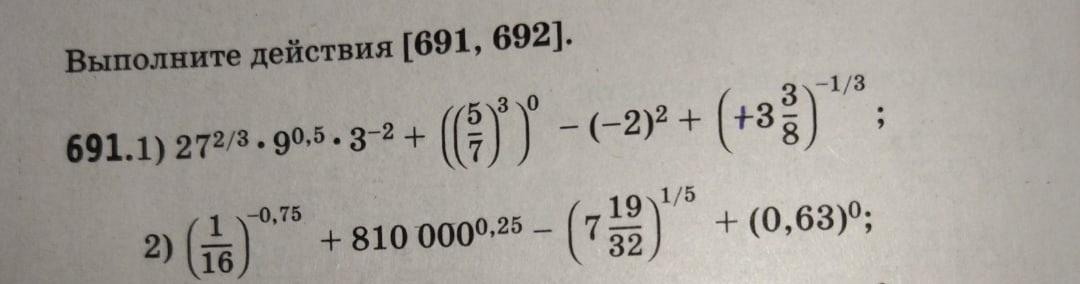
Avantgardе:
в 691 в скобке - на + исправлен?
Да там +
Ответы
Автор ответа:
1
Любое число в нулевой степени (кроме нуля, но в скобке он не получится) даст 1, поэтому можно не считать и сразу дать ответ
Спасибо
Похожие вопросы
Предмет: Английский язык,
автор: anastasiamilly
Предмет: Английский язык,
автор: daniil20052
Предмет: Русский язык,
автор: виктория587
Предмет: Геометрия,
автор: Marmes
Предмет: Математика,
автор: riska14