Question

Основанием прямой призмы является равносторонний треугольник. Найдите объем призмы, если ее сечение, проходящее через сторону основания и середину противолежащего бокового ребра, наклонено к плоскости основания под углом 60 градусов и площадь сечения равна 8$\sqrt{3}$.

Answer 1

Ответ:

48√3 куб. ед.

Объяснение:

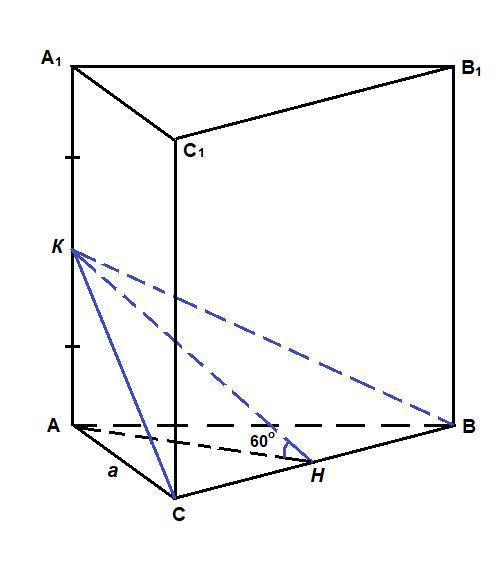
Пусть Н - середина ВС.

Тогда АН - медиана и высота треугольника АВС, так как он правильный,

АН⊥ВС.

АН - проекция КН на плоскость АВС, значит

КН⊥ВС по теореме о трех перпендикулярах.

∠KHA = 60° - угол между плоскостью сечения и основанием.

$S_{KBC}=\dfrac{1}{2}BC\cdot KH=8\sqrt{3}$

Пусть а - сторона основания.

$a\cdot KH=16\sqrt{3}$      (1)

$AH=\dfrac{a\sqrt{3}}{2}$  как высота равностороннего треугольника.

ΔКНА:  ∠КАН = 90°

$\cos\angle KHA=\dfrac{AH}{KH}$

$KH=\dfrac{AH}{\cos 60^\circ}=\dfrac{a\sqrt{3}}{2}:\dfrac{1}{2}=\dfrac{a\sqrt{3}}{2}\cdot \dfrac{2}{1}=a\sqrt{3}$

Подставим в (1):

a · a√3 = 16√3

a²√3 = 16√3

a² = 16

a = 4   (a = - 4 не подходит по смыслу задачи)

$AH=\dfrac{4\sqrt{3}}{2}=2\sqrt{3}$

ΔKHA:  ∠KAH = 90°,

$tg\angle KHA=\dfrac{AK}{AH}$

$AK=AH\cdot tg60^\circ=2\sqrt{3}\cdot \sqrt{3}=6$

$AA_1=2AK=12$

$S_{ABC}=\dfrac{a^2\sqrt{3}}{4}=\dfrac{16\sqrt{3}}{4}=4\sqrt{3}$

Объем призмы:

$V=S_{ABC}\cdot AA_1$

$V=4\sqrt{3}\cdot 12$

$V=48\sqrt{3}$