Предмет: Алгебра,
автор: 8888moon
найдите все значения x, при которых неравенство *на фото* обращается в равенство
Приложения:
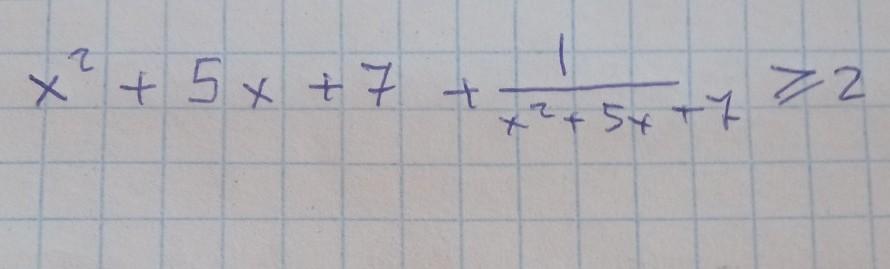
Ответы
Автор ответа:
1
Ответ:
Объяснение:
ОДЗ: знаменатель не может быть равен нулю.
Замена:
Обратная замена:
Похожие вопросы
Предмет: Українська мова,
автор: ЖеняХрущ
Предмет: Русский язык,
автор: albinagoloboko2
Предмет: Русский язык,
автор: галя2607
Предмет: Математика,
автор: xayrullaev06
Предмет: Математика,
автор: NikaPik