Предмет: Алгебра,
автор: bubaq20
ПОМОГИТЕЕЕ Пределы не пойму как решать. Переменные a, n, m - неизвестные, с ними нужно возится до конца
Приложения:
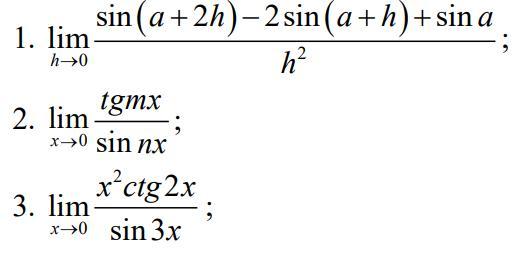
Ответы
Автор ответа:
1
Ответ:
Похожие вопросы
Предмет: Русский язык,
автор: BonpocHuK1
Предмет: Русский язык,
автор: Аноним
Предмет: Окружающий мир,
автор: tonyti
Предмет: Литература,
автор: жкхопр09872453