Предмет: Алгебра,
автор: tent1266
помогите пожалуйста срочно
Приложения:
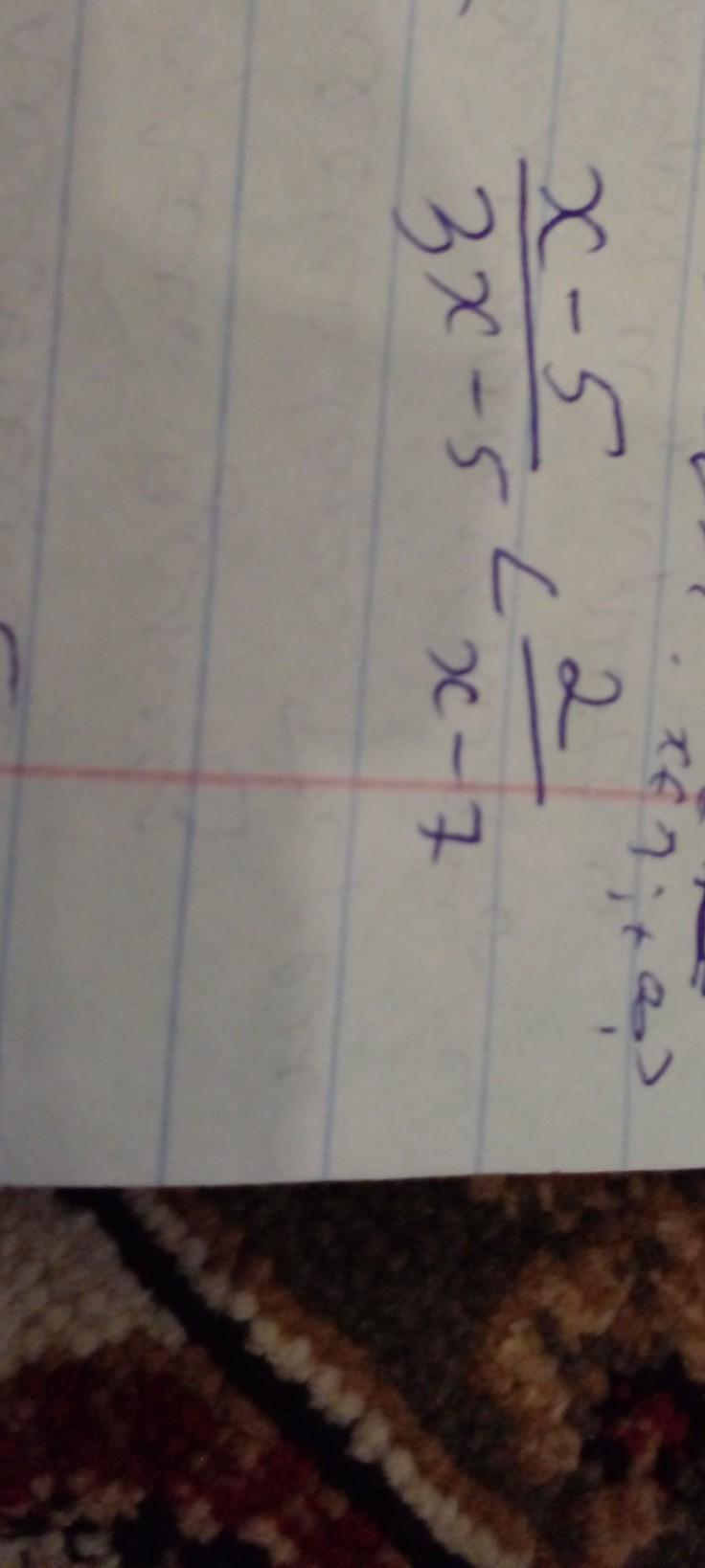
Ответы
Автор ответа:
1
Объяснение:
ОДЗ:
3x-5≠0 3x≠5 |:3 x≠1²/₃ x-7≠0 x≠7.
-∞__+__1²/₃__-__3__+__7__-__15__+__+∞ ⇒
Ответ: x∈(1²/₃;3)U(7;15).
Похожие вопросы
Предмет: Русский язык,
автор: витмоно1
Предмет: Русский язык,
автор: ник2093
Предмет: Русский язык,
автор: adelyar75
Предмет: Математика,
автор: koklofdf