Question

Пожалуйста,помогите!!!
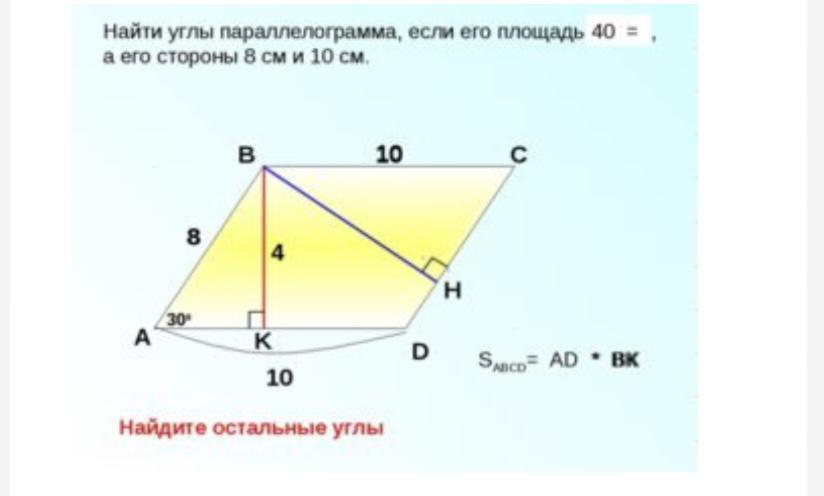
SABCD= AD * BК Найти углы параллелограмма, если его площадь 40 см2, а его стороны 8 см и 10 см.

Answer 1

Объяснение:

Площадь параллелограмма ABCD определяется произведением его высоты (h) на основание. В условии не определено какая из сторон является основанием, поэтому можно выбрать ту, которая удобнее для расчета. Определим высоту параллелограмма для основания, равного 10 см:

h = S / 10 = 40 / 10 = 4 см.

Высота, боковая сторона параллелограмма и часть основания образуют прямоугольный треугольник, в котором высота, являющаяся катетом, равна 4 см, а гипотенуза составляет 8 см. Их отношение определяет синус угла при основании параллелограмма (угла, противоположного высоте). Обозначим этот угол A, гипотенузу АВ, а высоту ВН, тогда:

sin A = BH / AB = 4/8 = 1/2.

Известно, что 1/2 соответствует sin 30⁰, следовательно угол:

<А = 30⁰;

Так как стороны параллелограмма попарно параллельны, а углы, прилегающие к одной его стороне, составляют 180⁰, угол В составит:

<В = 180⁰ - 30⁰ = 150⁰;

При этом углы параллелограмма попарно равны, значит углы <A и <C составляют 30⁰, а углы <B и <D равны 150⁰

Answer 2

Ответ:

30°; 150°; 30°; 150°

Объяснение:

Сумма углов прилежащих к одной стороне параллелограма равна 180°

<А+<В=180°

<В=180°-<А=180°-30°=150°

Противоположные углы параллелограма равны.

<А=<С=30°

<В=<D=150°

Ответ: 30°; 150°; 30°; 150°