Пожалуйста, помогите!
Найти площадь параллелограмма. АBCD - параллелограмм.
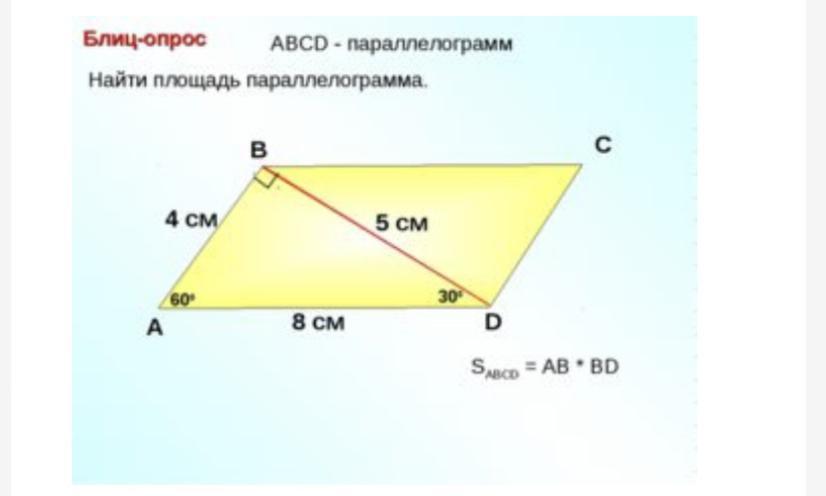
Ответы
Ответ:
Задача некорректно составлена. Решения нет.
Объяснение:
Используем угол между сторонами.
Площадь параллелограма равна произведению двух смежных сторон на синус угла между этими сторонами.
S(ABCD)=АВ*АD*sin<A
sin60°=√3/2
S(ABCD)=4*8*√3/2=16√3 см²
Ответ: 16√3см²
_______
Используем площадь треугольника ∆АВD. (Через стороны АВ и BD)
S(∆ABD)=1/2*4*5=10см²
Диагональ параллелограма делит параллелограм на два равновеликих треугольника.
S(ABCD)=2*S(∆ABD)=2*10=20см².
Ответ: 20см²
_________
Рассмотрим треугольник ∆АВD.
∆ABD- прямоугольный треугольник.
АВ; ВD- катеты.
АD- гипотенуза.
По теореме Пифагора
АD=√(AB²+BD²)=√(4²+5²)=√41 что не соответствует действительности. Т.к. по условию AD=8; .
Прямоугольного треугольника с такими сторонами не существует. Также как и параллелограма.