При измерении активного сопротивления резистора были произведены десять равноточных измерений, результаты которых приведены в таблице. Оцените максимальную и относительную погрешности и запишите результат измерения для доверительных вероятностей 0,95 и 0,99.
8.243 8.248 8.244 8.249 8.247 8.242 8.244 8.248 8.247 8.243
Ответы
Ответ:
Объяснение:
Задачи по "Математической статистике" лучше всего выполнять при помощи Excel.
1)
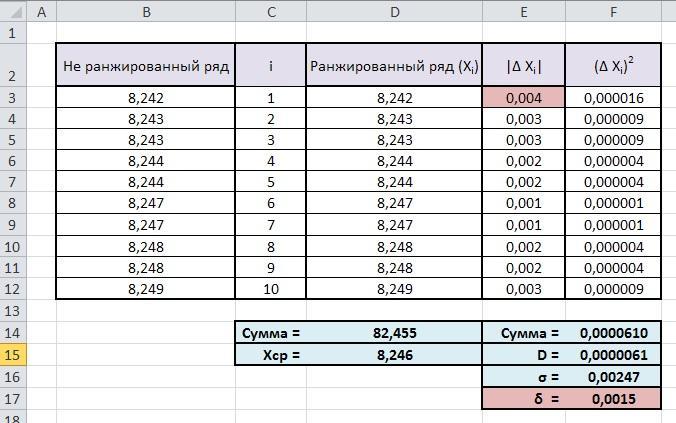
Заносим данные в столбец B, назвав его "Не ранжировнный ряд".
В столбец С - индексы i от 1 до 10.
Автоматически сортируем данные по возрастанию (столбец D). Назовем его "Ранжированный ряд Xi. Ранжированный - значит упорядоченный.
2)
В нижнюю таблицу помещаем сумму элементов Xi (Excel, конечно, подсчитает по формуле СУММ)
∑ Xi = 82,455
Находим среднее значение сопротивления:
Xcp = ∑ Xi / n = 82,455 / 10 ≈ 8,246
3)
Вернемся к верхней таблице.
В столбце Е находим модуль абсолютной ошибки:
ΔXi = Xi - Xcp
Сразу получили максимальную погрешность:
Δmax = 0,004
Относительная погрешность:
ε = Δmax / Xcp = 0,004 / 8,286 ≈ 0,0005
4)
Теперь найдем результат измерения сопротивления для доверительной вероятности γ = 0,95.
Для этого опять будем работать в верхней таблице.
В столбце D - квадраты относительных погрешностей.
Суммируем:
Σ (ΔXi)² = 0,0000610
Находим дисперсию:
D = Σ (ΔXi)² / n = 0,0000061
Находим квадратическое отклонение:
σ = √ (D) = √ (0,0000061) ≈ 0,0027
Из справочника находим tγ при n=10 и γ = 0,95
tγ = 1,96
И тогда находим погрешность измерений сопротивления:
δ = tγ·σ / √(n) = 0,0015
Результат:
8,246 - 0,0015 < R < 8,246 + 0,0015
Аналогично и при γ = 0,99 по этому алгоритму решить задачу...