Предмет: Математика,
автор: andreisaa06
Помогите решить до 10.11.2021
Приложения:
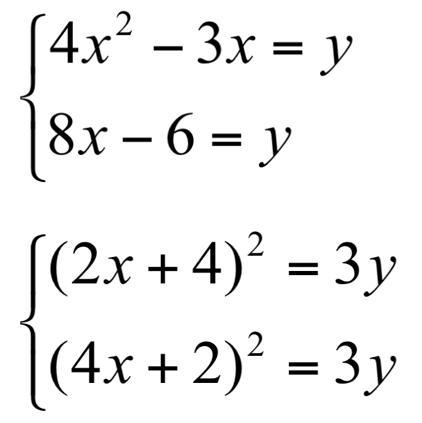
Ответы
Автор ответа:
0
т.к. левая часть уравнений = y, то можно их приравнять
Ответ: ( x1; y1) = ( 0.75; 0)
( x2; y2) = ( 2; 10)
также приравниваем
обе части делим на 12
Ответ: ( x1; y1) = ( -1; 0.75)
( x2; y2) = ( 1; 12)
Очень подробно рассписал, надеюсь помог
Похожие вопросы
Предмет: Русский язык,
автор: Masha20071
Предмет: Английский язык,
автор: polin7275
Предмет: Русский язык,
автор: TatyanaMiss
Предмет: Литература,
автор: Дашуня75