Предмет: Алгебра,
автор: magomedov5679
Ребята срочно нужна помощь[]
Выполните все 4 с дискоминатом 9кл подготовка к йоге и тд
Спасибки
Приложения:

Ответы
Автор ответа:
1
Ответ:
Объяснение:
Первое уравнение не решается дискриминантом ,так как нет переменной C ,а значит нужно решать способом разложения ,то-есть как на изображении :
Прошу выбрать лучший из ответов и оценить его ,если согласны и довольны им .
Приложения:

Автор ответа:
1
Объяснение:
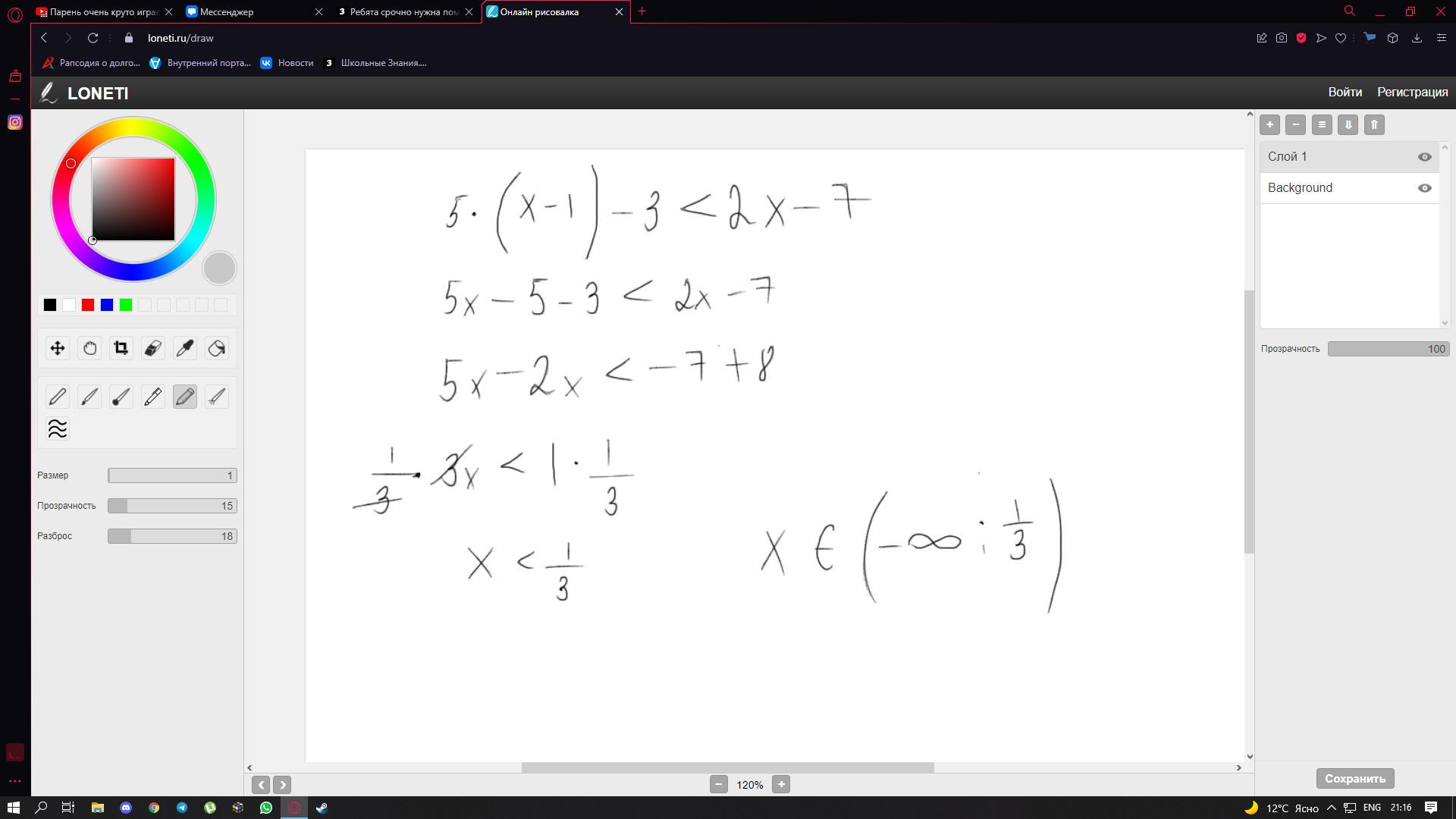
1.
Решим через дискриминант:
Где a = 3, b = - 15, c =0
Дискриминант > 0, а это значит имеет 2 корня
И
Найдем корни:
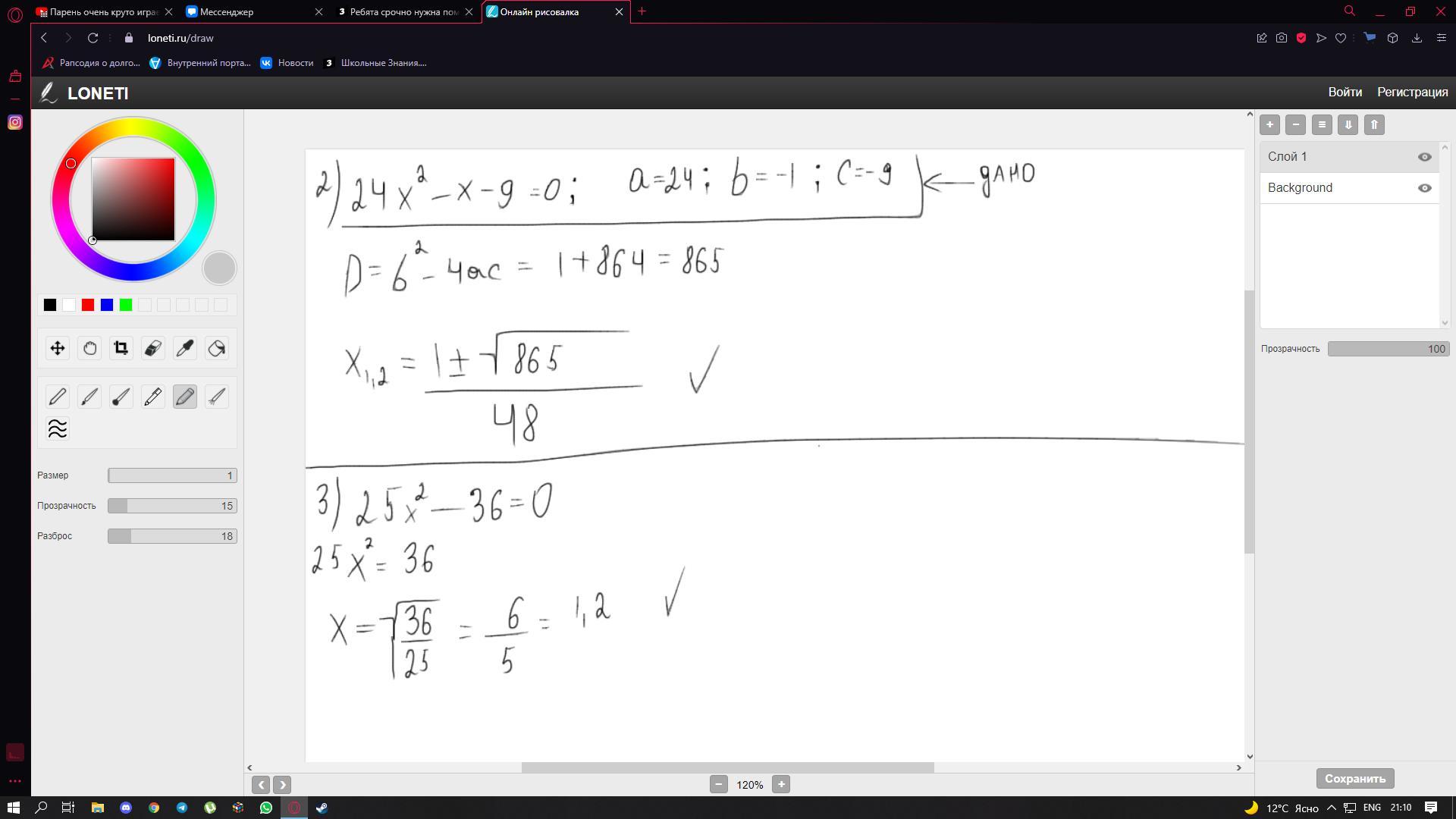
2.
3.
4.
Данное уравнение не является квадратным. Потому дискриминант не возможен.
Похожие вопросы
Предмет: Английский язык,
автор: Аноним
Предмет: Русский язык,
автор: 7smj
Предмет: Русский язык,
автор: bakaevedil
Предмет: Английский язык,
автор: Аноним
Предмет: Математика,
автор: fufik19