Предмет: Математика,
автор: Аноним
помогите пожалуйста
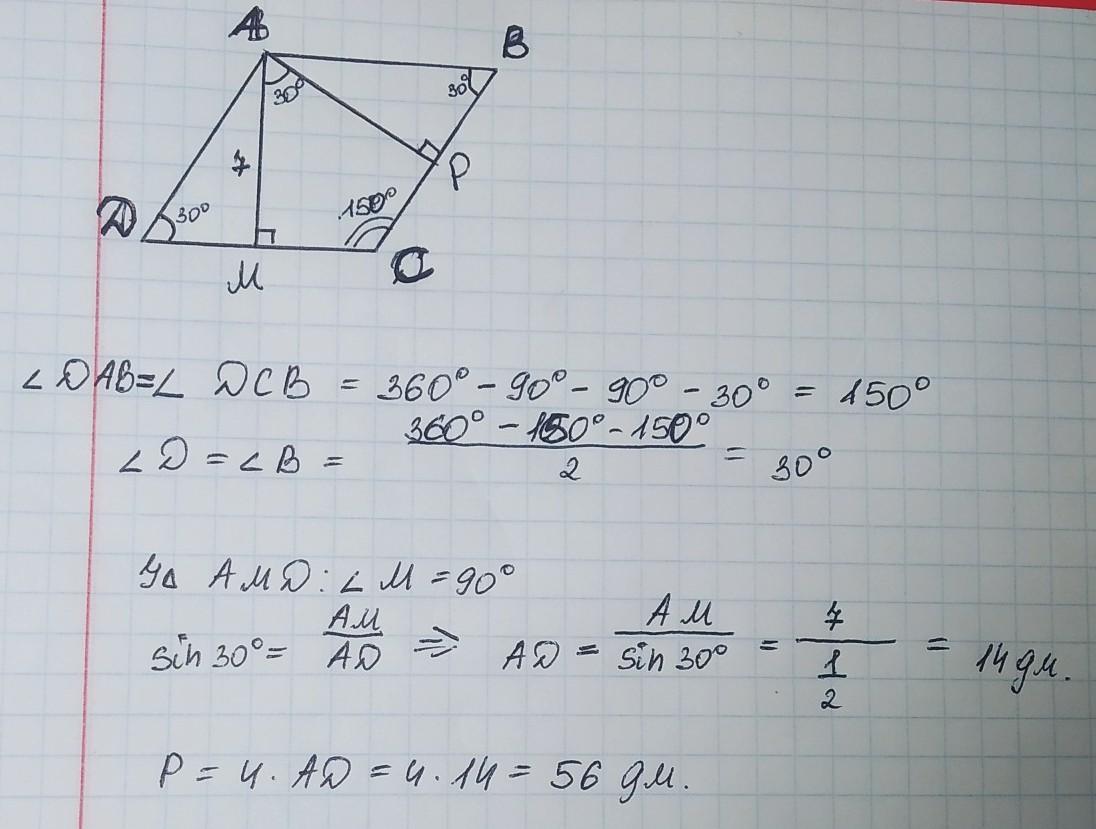
в ромбе ABCD с вершины тупого угла А проведены высоты AM и АР к сторонам DC и BC соответственно. Найдите периметр ромба, если АМ = 7дм, угол МАР = 30°
Ответы
Автор ответа:
1
Вот, держи мой ответ, пожалуйста)
Приложения:
Автор ответа:
1
Сума углов четырёхугольника = 360°
Так как AM и AP - высоты, то углы AMC, AMD, APC и ABC будут по 90°
Угол C = 360° - угол AMC - угол APC - угол MAP = 150°
В ромбе противоположные углы равны(угол C = углу A = 150°)
Углы MAD и PAB - равны
Пусть углы MAD и PAB - x
Тогда: x + x + 30° = 150°
x = 60°
Так как MAD прямоугольный треугольник, угол ADM = 180° - угол AMD - угол MAD = 30°
Катет лежащий против угла 30° равен половине гипотенузы
Тогда AD = 2 × AM = 14(дм)
У ромба все стороны равны
P = 4 × a = 4 × 14 = 56(дм)
Ответ: P = 56 дм
Приложения:

Kaldapol:
@mr_rulia
а зачем
угол MAD + угол BAP = 150° - 30°
эти углы равны
значит MAD + BAP = 120
MAD = BAP = 60°
Похожие вопросы
Предмет: Окружающий мир,
автор: Mistik3111111111
Предмет: Русский язык,
автор: Lolkaxc
Предмет: Русский язык,
автор: БАКЛАЖАН666
Предмет: Геометрия,
автор: vvvvvvvvvvv56
Предмет: Русский язык,
автор: Аноним