Question

y=(x-1)^2/x^2+1 исследовать функцию и построить график

Answer 1

Пошаговое объяснение:

$\displaystyle y=\frac{(x-1)^2}{x^2+1}$

1. ОДЗ: $x\in{R}$

2.Четность, нечетность:

$\displaystyle y(-x)=\frac{(-x-1)^2}{(-x)^2+1} =\frac{(x+1)^2}{x^2+1}\\\\y(-x)\neq y(x)\neq -y(x)$

⇒ функция не является четной или нечетной, то есть общего вида.

3. пересечение с осями:

x=0 ⇒  у=1;

у=0 ⇒ (х-1)² = 0; х=1

4. Асимптоты.

Вертикальных асимптот нет.

Наклонная: y = kx+b

$\displaystyle k= \lim_{x \to \infty} \frac{(x-1)^2}{x(x^2+1)}=0\\\\b = \lim_{x \to \infty} \frac{(x-1)^2}{x^2+1} = \lim_{x \to \infty} \frac{\frac{x^2}{x^2}-\frac{2x}{x^2}+\frac{1}{x^2} }{\frac{x^2}{x^2}+\frac{1}{x^2} }=1$

⇒ y=1 - горизонтальная асимптота.

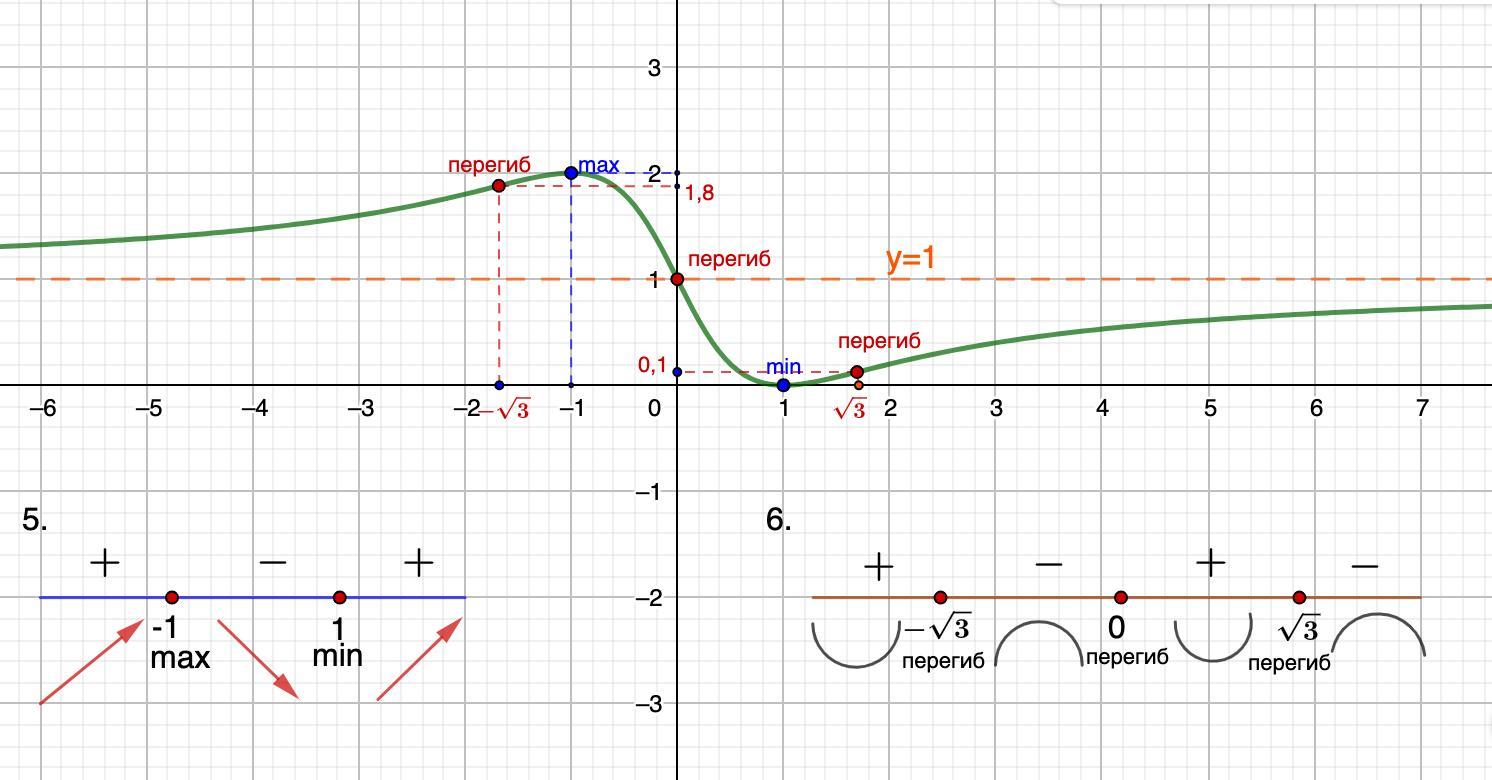
5. Возрастание, убывание. Экстремумы.

Найдем производную, приравняем к 0. Найдем корни, отметим на числовой оси, определим знак производной на промежутках.

Если "+", функция возрастает, "-" - убывает.

$\displaystyle y'=\frac{2(x-1)*(x^2+1)-(x-1)^2*2x}{(x^2+1)^2} =\\\\=\frac{2x^3+2x-2x^2-2-2x^3+4x^2-2x}{(x^2+1)^2} =\\\\=\frac{2x^2-2}{(x^2+1)^2} =\frac{2(x-1)(x+1)}{(x^2+1)^2} \\\\x_1=1;\;\;\;x_=-1$

См. рис.

$x_(max)=-1;\;\;\;x_{min}=1\\\\y(-1)=2;\;\;\;y(1)=0$

6. Выпуклость, вогнутость.

Найдем вторую производную, приравняем к 0. Найдем корни, отметим на числовой оси, определим знак второй производной на промежутках.

Если "+", функция вогнутая, "-" - выпуклая.

$\displaystyle y''=\frac{4x(x^2+1)^2-(2x^2-2)*2(x^2+1)*2x}{(x^2+1)^4} =\\\\=\frac{4x(x^2+1)-4x(2x^2-2)}{(x^2+1)^3} =\frac{4x^3+4x-8x^3+8x}{(x^2+1)^3} =\\\\=\frac{12x-4x^3}{(x^2+1)^3} =\frac{4x(\sqrt{3}-x)(\sqrt{3}+x) }{(x^2+1)^3} \\\\x_1=0;\;\;\;x_2=-\sqrt{3};\;\;\;x_3=\sqrt{3}$

Cм. рис.

В точках х=-√3; 0; √3    - перегиб

$y(0) = 1;\;\;\;y(-\sqrt{3})\approx 1,8;\;\;\;y(\sqrt{3})\approx 0,1$

Строим график .