Question

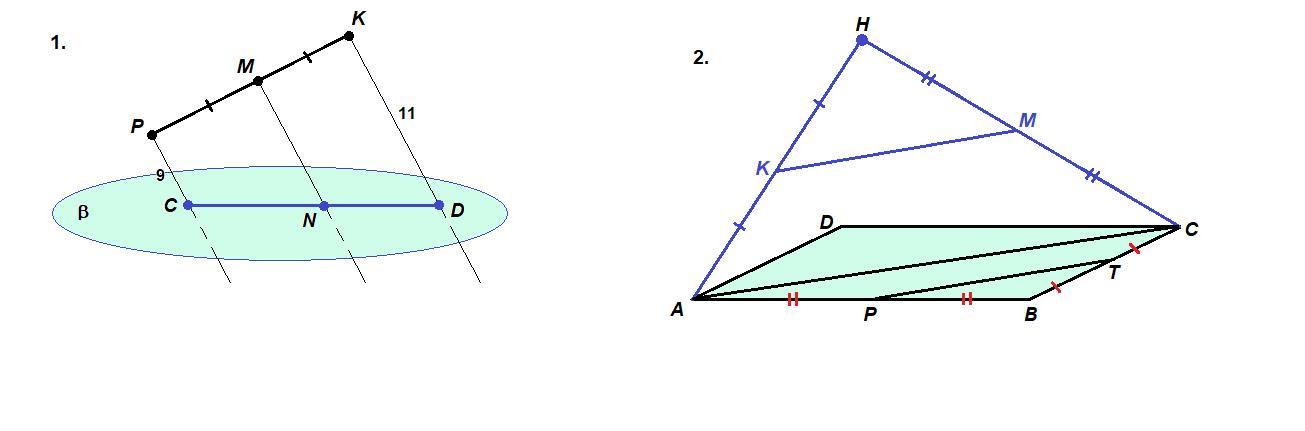
1)Через точки Р, К и середину М отрезка РК проведены параллельные прямые, пересекающие некоторую плоскость β в точках С, D, N соответственно. Найдите длину отрезка MN, если РС=9 м, КD=11 м, причем отрезок РК не пересекает плоскость β.
2)Точка Н не лежит в плоскости параллелограмма ABCD. Докажите, что прямая, проходящая через середины отрезков НА и НС, параллельна прямой, проходящей через середины сторон АВ и ВС параллелограмма.

Answer 1

Ответ:

1) MN = 10 м

Объяснение:

1)

Плоскость (СРК) пересекает плоскость β по прямой CD, которой принадлежат все их общие точки, т.е. точки C, D, N лежат на одной прямой.

РМ = МК, через точки проведены параллельные прямые, значит

CN = ND по теореме Фалеса.

Тогда MN - средняя линия трапеции CPKD (PC и KD - основания).

$MN=\dfrac{PC+KD}{2}=\dfrac{9+11}{2}=10$ м

2)

КМ║АС как средняя линия треугольника АНС,

РТ║АС как средняя линия треугольника АВС, значит КМ║РТ.