Помогите решить уравнение
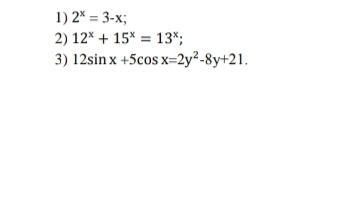
Ответы
Ответ:
Объяснение:
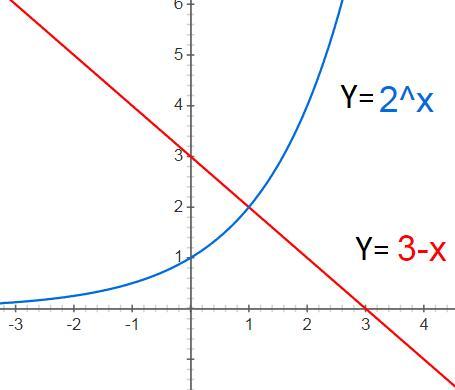
1) 2ˣ=3-х
решим графически
построим график y=2ˣ и у=3-х и найдем точку пересечения
х=1
2) 12ˣ+15ˣ=13ˣ
12ˣ+15ˣ-13ˣ=0
а) при х>0 15ˣ>13ˣ ⇒ 15ˣ-13ˣ>0 ⇒ 12ˣ+15ˣ-13ˣ>0 ⇒ корней нет
б) при х=0 12+15=27≠13
в) при х<0 12ˣ>13ˣ ⇒ 12ˣ-13ˣ>0 ⇒ 12ˣ+15ˣ-13ˣ>0 ⇒ корней нет
Уравнение не имеет решений
3)
решим как квадратное уравнение
2y²-8y+21 -12sinx-5cosx=0
D=64-4*2*(21 -12sinx-5cosx)=
=8(8-21+12sinx+5cosx)=8(12sinx+5cosx-13)
=8*13((12/13)sinx+(5/13)cosx-1)
также как при решении уравнения вида asinx+bcosx=c
сделаем замену cosφ=12/13 ; sinφ=5/13
тогда tgφ=5/12
φ=arctg(5/12)+пm, m∈Z
(12/13)sinx+(5/13)cosx=сosφsinx+sinφcosx=sin(x+φ)
D=8*13(sin(x+φ)-1)
с учетом того что sinx≤1
уравнение имеет решение только при sin(x+φ)=1 и тогда D=0
тогда
(12/13)sinx+(5/13)cosx=1 ⇒
12sinx+5cosx=13 и исходное уравнение примет вид
2y²-8y+21 -12sinx-5cosx=0
2y²-8y+21 -13=0
2y²-8y+8=0
y²-4y+4=0
(y-2)²=0
y=2
решим sin(x+φ)=1 это частный случай
x+φ=(п/2)+2kп , k∈Z
x=(п/2)-φ+2kп
x=(п/2)-arctg(5/12)+пm+2kп; m,k∈Z
таким образом уравнение имеет бесконечное множество решений
x=(п/2)-arctg(5/12)+пm+2kпm,k∈Z ; y=2 ;