Предмет: Алгебра,
автор: VarvaraZubanova
Здравствуйте. Мне нужна помощь с заданиями..
Приложения:

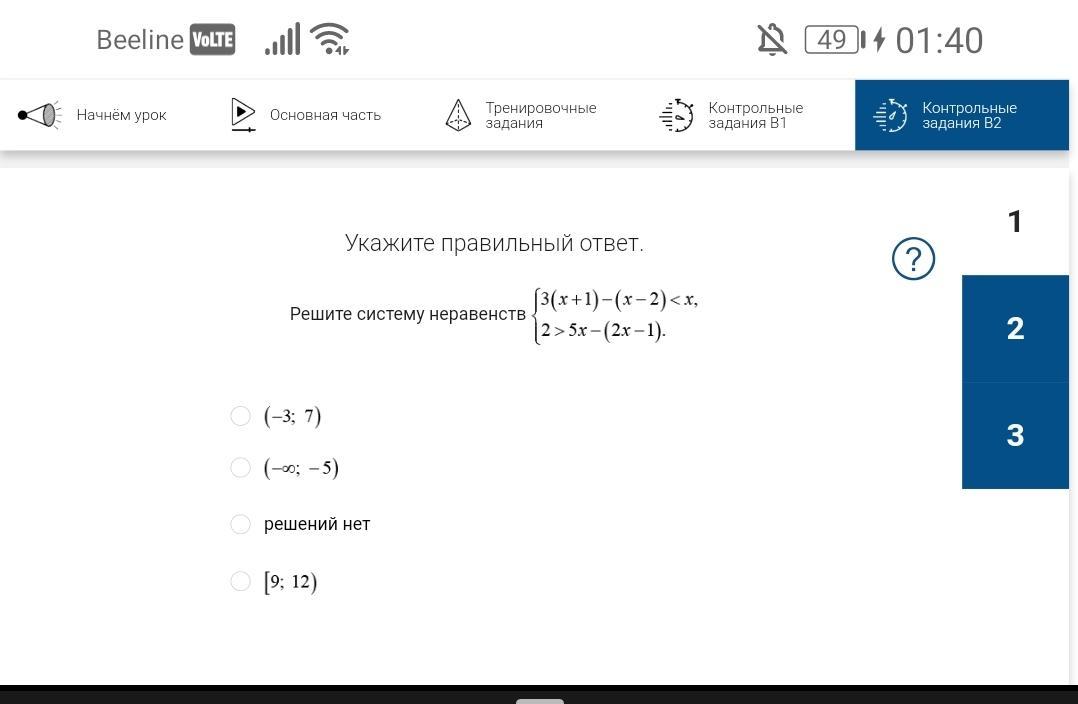
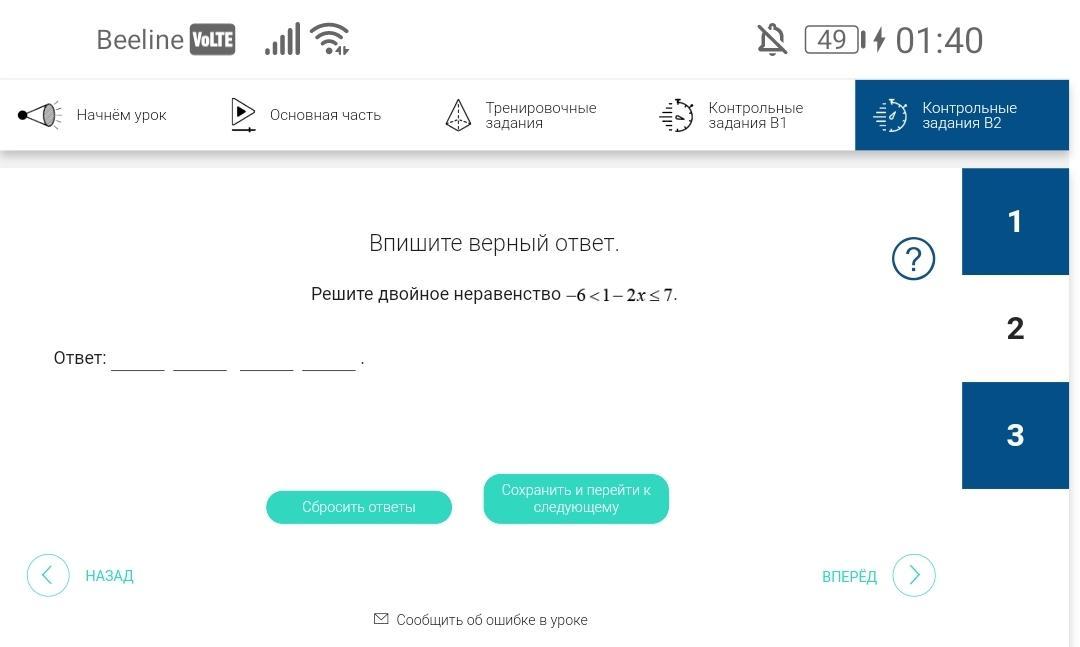
Ответы
Автор ответа:
1
Ответ:
Ни при каких значениях переменной "х" значения функций не будут одновременно принимать отрицательные значения .
Похожие вопросы
Предмет: Русский язык,
автор: BonAnette
Предмет: Окружающий мир,
автор: ira12345678901213141
Предмет: Другие предметы,
автор: дадал1
Предмет: Биология,
автор: STEL1337
Предмет: Математика,
автор: dayana7137