Question

Вариант 4
Задача 1
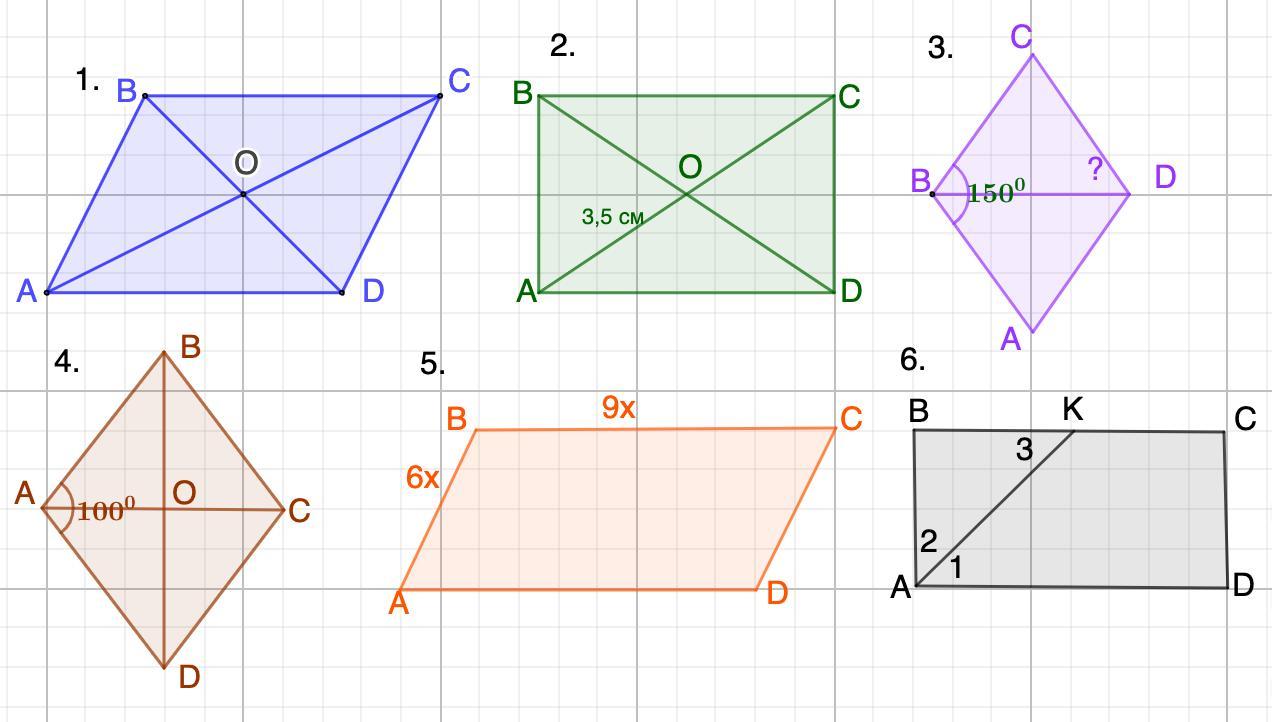
⦁ В параллелограмме АВСД диагонали пересекаются в точке О, ВД=28см. Найдите ВО.

А) 7 см; Б) 5 см; В) 3,5 см; Г) 14 см.
Задача 2
⦁ В прямоугольнике АВСД диагонали пересекаются в точке О, АО=3,5см. Найдите ВД.

А) 7 см; Б) 5 см; В) 3,5 см; Г) 14 см.
Задача 3
⦁ В ромбе АВСД ےАВС=150°. Чему равен ےВДС.

А) 70°; Б) 35°; В) 20°; Г) 60°.
Задача 4
⦁ В ромбе АВСД диагонали пересекаются в точке О, ےА=100°. Определите углы треугольника АДО.

А) 45°; 45°; 90°; Б) 30°; 60°; 90°;

В) 55°; 35°; 90°; г) 40°; 50°; 90°.
Задача 5
⦁ Стороны параллелограмма относятся как 9 : 6. Найдите его периметр, если разность его сторон равна 15см.
Задача 6
⦁ Биссектриса угла А прямоугольника АВСД делит сторону ВС на отрезки 7см и 3см. Каким может быть периметр прямоугольника? (2 случая)


Можно решение этих задач? Хотя бы 3-4 задания кто может.

Answer 1

Объяснение:

1. BD = 28 см  - диагональ.

В параллелограмме диагонали точкой пересечения делятся пополам.

⇒ ВО = 28:2 = 14 (см)

2. АО = 3,5 см

В прямоугольнике диагонали точкой пересечения делятся пополам.

⇒ АС = 3,5 ·2 = 7 (см)

В прямоугольнике диагонали равны.

АС = BD = 7 см

3. ∠АВС = 150°

В ромбе противоположные углы равны.

⇒ ∠АВС = ∠D = 150°

Диагонали ромба являются биссектрисами его углов.

∠BDC = ∠D : 2 = 150° : 2 = 75°

(ответа такого нет. Проверьте условие)

4. ∠А = 100°

Диагонали ромба являются биссектрисами его углов.

⇒ ∠OAD = ∠A :2 = 100° : 2 = 50°

Диагонали ромба перпендикулярны.

⇒ ΔАDO - прямоугольный, то есть

∠АОD = 90°

Сумма острых углов прямоугольного треугольника равна 90°.

⇒ ∠ АDO = 90° - 50° = 40°

5. ВС : АВ = 9:6

Пусть АВ = 6х, тогда ВС = 9х.

⇒ 9х - 6х = 15 (см)

3х = 15

х = 5

⇒ АВ = 30 см; ВС = 45 см

Периметр параллелограмма равен удвоенной сумме смежных сторон.

Р = 2 ·(АВ+ВС) = 2·(30+45) = 150 (см)

6. АК - биссектриса

⇒ ∠ВАК = ∠KAD =45°

Рассмотрим ΔАВК.

Сумма острых углов прямоугольного треугольника равна 90°.

⇒ ∠ВКА = 90°-45° = 45°

⇒ ΔАВК - равнобедренный (углы при основании равны)

АВ = ВК

а) ВК = 7 см; КС = 3 см.

ВК=АВ = 7 см; ВС = 7+3 = 10 (см)

Периметр прямоугольника равен удвоенной сумме смежных сторон.

Р = 2(7+10) = 34 (см)

б) ВК = 3 см; КС = 7 см.

ВК=АВ = 3 см; ВС = 7+3 = 10 (см)

Р = 2(3+10) = 26 (см)