Question

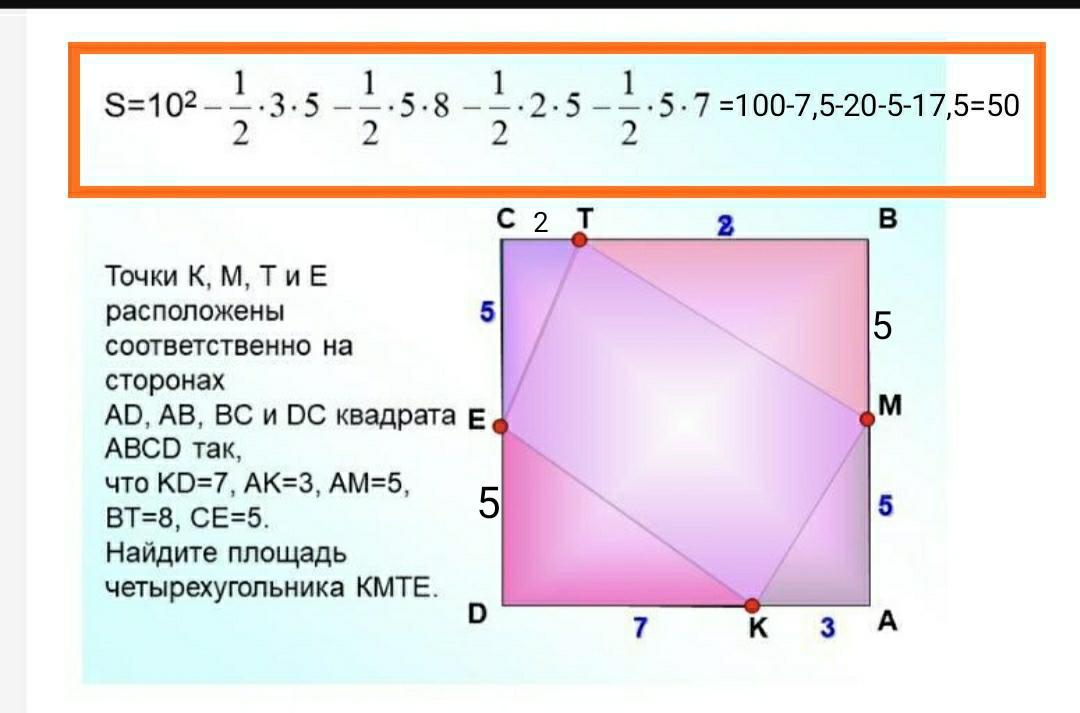
Точки К, М, Т и Е расположены соответственно на сторонах
АD, AB, BC и DC квадрата АВСD так,
что KD=7, AK=3, AM=5,
BT=8, CE=5.
Найдите площадь четырехугольника КМТЕ.

Answer 1

Ответ:

50ед²

Объяснение:

Сторона квадрата ABCD равна.

DA=DK+KA=7+3=10ед.

S(ABCD)=DA²=10²=100ед²

S(∆KAM)=1/2*KA*AM=1/2*3*5=7,5ед².

BM=AB-MA=10-5=5ед

S(∆МВТ)=1/2*ВМ*ТВ=1/2*8*5=20ед²

СТ=СВ-ТВ=10-8=2ед.

S(∆TCE)=1/2*TC*CE=1/2*5*2=5ед²

ЕD=CD-CE=10-5=5ед.

S(∆EDK)=1/2*ED*DK=1/2*7*5=17,5ед²

S(KMTE)=S(ABCD)-S(∆KAM)-S(∆MBT)-

-S(∆TCE)-S(∆EDK)=100-7,5-20-5-17,5=

=50ед²

Answer 2

Ответ:

50

Объяснение:

СВ=АD

СТ=(DK+AK) - TB=(7+3)-8=2

AB=AD=DK+AK=7+3=10

BM=AB-AM=10-5=5

DC=AD

DE=DC-CE=10-5=5

S=Sкв-S1-S2-S3-S4=

=10^2-1/2×CT×CE-1/2×BM×TB-

-1/2×AK×AM-1/2×DK×DE=

=100-1/2×2×5-1/2×5×8-1/2×3×5-1/2×7×5=

=100-5-20-7,5-17,5=50 (ед^2)