Question

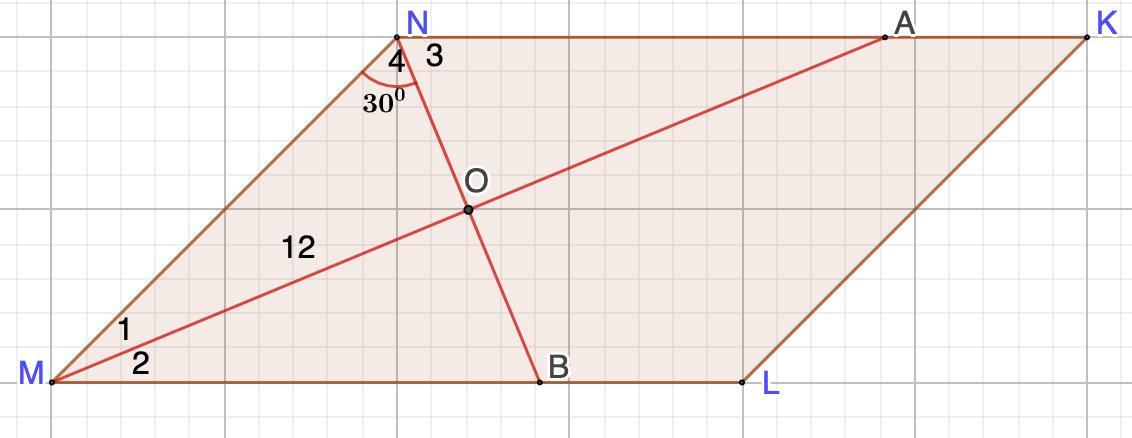
В параллелограмме MNKL биссектрисы углов М и N пересекаются в точке 0 таким образом, что МО = 12 и MN0 – 30°. Найди сторону MN. СРОЧНО ​пожалуйста. ЧИСТЫЙ ОТВЕТ БЕЗ РЕШЕНИЯ

Answer 1

Ответ:

24 ед.

Объяснение:

Дано: MNKL - параллелограмм;

MA и NB - биссектрисы.

МО = 12; ∠MN0 = 30°

Найти: MN

Решение:

В параллелограмме сумма углов, прилежащих к одной стороне, равна 180°.

⇒ ∠M + ∠N = 180°

∠1=∠2; ∠3=∠4 (MA и NB - биссектрисы)

⇒ ∠1+∠2+∠3+∠4 = 180°

или ∠1+∠4 = 90°

Рассмотрим ΔMNO.

Сумма углов треугольника равна 180°.

⇒ MON = 180° - 90° = 90°

то есть ΔMNO - прямоугольный.

Катет, лежащий против угла в 30°, равен половине гипотенузы.

⇒ NM = 2 MO = 2*12 = 24.