Предмет: Математика,
автор: caltri
Помогите пожалуйста, Задание:Разобрать решения
Приложения:


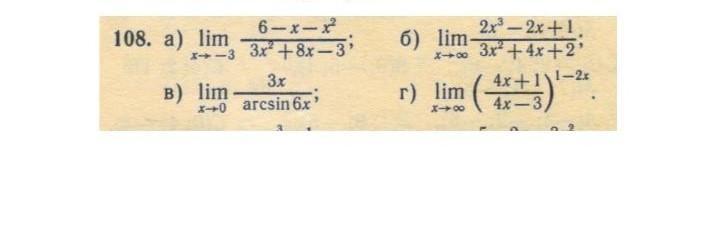
caltri:
первые две фото пример решить надо примеры под 108 номером
Ответы
Автор ответа:
0
Ответ:
а) -1/2 б) бесконечность в) 1/2 г) 1/е^2
Пошаговое объяснение:
а)
Подставляя n=-3, получаем ответ -1/2
б).
в) arcsin6x=y
6x=siny
.
г)
Похожие вопросы
Предмет: Русский язык,
автор: ариман1
Предмет: Русский язык,
автор: гончарова1234567890
Предмет: Другие предметы,
автор: MARISOVA
Предмет: Алгебра,
автор: AndronovEZ
Предмет: Математика,
автор: kurashastitch