Предмет: Математика,
автор: Аноним
Найти наибольшее и наименьшее значение функции на отрезке.
Если можно, то с объяснением.
Приложения:
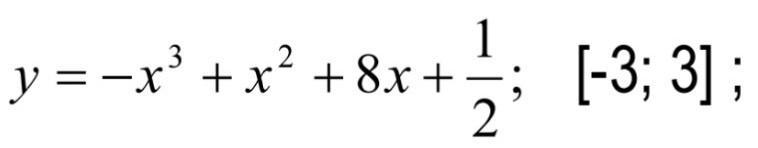
Ответы
Автор ответа:
1
Привет)
daniilzhulanov:
сделал
Похожие вопросы
Предмет: Українська мова,
автор: хел1
Предмет: Русский язык,
автор: likarnazar1608
Предмет: Окружающий мир,
автор: maskarowanadia
Предмет: Математика,
автор: vnqmi
Предмет: Физика,
автор: daniktsarev