Предмет: Алгебра,
автор: badirovaslan12
Срочно, развёрнутый ответ
Приложения:
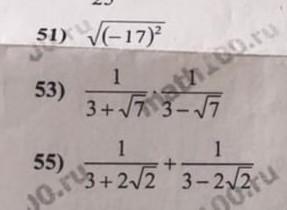
Ответы
Автор ответа:
1
Ответ:
51) 17
53) 0,5
54) 6
Объяснение:
51)
Т.к. извлекаем квадратный корень (корень чётной степени), то не забываем ставить модуль, т.к.
53)
Перемножаем дроби, в знаменателе применяем формулу разности квадратов: (a-b)(a+b)=a²-b²
55)
Складываем дроби, общий множитель:
Дополнительный множитель к первой дроби
Дополнительный множитель ко второй дроби
Далее, в числителе приводим подобные члены, получаем 6, в знаменателе используем формулу разности квадратов:
(a-b)(a+b)=a²-b²
Похожие вопросы
Предмет: Русский язык,
автор: nukekg
Предмет: Другие предметы,
автор: 28ayson
Предмет: Другие предметы,
автор: Маытуна
Предмет: Русский язык,
автор: Bloomberry