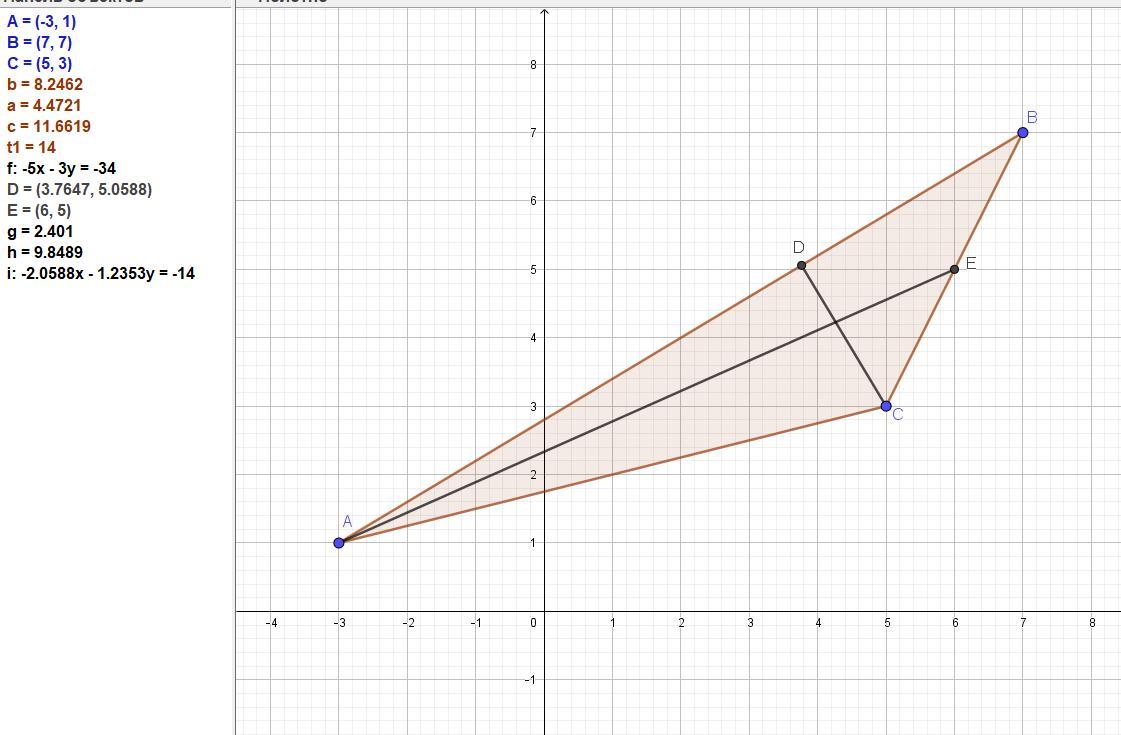
Задан трикутник АВС координатами своїх вершин : А(-3,1) ; В(7,7) ; С(5,3) .Записати рівняння сторін АВ і АС та знайти їх довжину ; знайти кутові коефіцієнти сторін АВ і АС та кут між сторонами АВ і АС ; записати рівняння медіани АЕ та знайти її довжину ; записати рівняння висоти СD та знайти її довжину.
Ответы
Задан трикутник АВС координатами своїх вершин: А(-3; 1); В(7; 7); С(5; 3).
1) Записати рівняння сторін АВ і АС та знайти їх довжину ;
Находим векторы АВ и АС.
АВ = (7-(-3); 7-1) = (10; 6), модуль равен √(10² + 6²) = √(100 + 36) = √136 = 2√34 ≈ 11,6619.
АС = (5-(-3); 3-1) = (8; 2), модуль равен √(8² + 2²) = √(64 + 4) = √68 = 2√17 ≈ 8,2462.
Уравнение АВ: (x + 3)/10 = (y - 1)/6 каноническое.
6x + 18 = 10y - 10,
6x - 10y + 28 = 0 или 3x - 5y + 14 = 0 общего вида,
y = (6/10)x + (28/10) или y = 0,6x + 2,8 с угловым коэффициентом.
Уравнение АС: (x + 3)/8 = (y - 1)/2 каноническое.
2x - 8y + 14 = 0 или x - 4 y + 7 = 0 общего вида.
у = (1/4)x + (7/4) с угловым коэффициентом.
2) знайти кутові коефіцієнти сторін АВ і АС та кут між сторонами АВ і АС ;
Угловые коэффициенты определены выше:
к(АВ) = 6/10 = 3/5 = 0,6.
к(АС) = 1/4 = 0,25.
cos(AB_AC) = (10*8 + 6*2)/(2√34*2√17) = 92/(68√2) = 23√2/34 ≈ 0,95667.
Угол А = arccos 0,95667 = 16,928 градуса.
3) записати рівняння медіани АЕ та знайти її довжину ;
Находим координаты точки Е как середины стороны ВС.
Е = (В(7; 7) + С(5; 3))/2 = (6; 5), модуль равен √(6² + 5²) = √(36 + 25) = √61.
Уравнение АЕ: (x + 3)/6 = (y - 1)/5.
5x- 6y + 21 = 0.
y = (5/6)x + (21/6).
4) записати рівняння висоти СD та знайти її довжину.
В уравнении общего вида высоты CD как перпендикуляра к АВ коэффициенты А и В меняются на -В и А.
CD: 5x + 3y + C = 0 , чтобы определить слагаемое С подставим координаты точки С: 5*5 + 3*3 + С = 0, отсюда С =-25 - 9 = -34.
Уравнение CD: 5x + 3y - 34 = 0.
Находим основание высоты CD как точку её пересечения со стороной АВ.
CD: {5x + 3y - 34 = 0|x(5) = 25x + 15y - 170 = 0
AB: {3x - 5y + 14 = 0 |x(3) = 9x - 15y + 42 = 0
34x - 128 = 0
x = 128/34 = 64/17 ≈ 3,7647.
y = (3x + 14)/5 = ((3*(64/17)) + 14)/5 = 86/17 ≈ 5,0588.
По разности координат находим CD = 2,401.