ДАЮ 35 БАЛЛОВ, ОЧЕНЬ НУЖНО
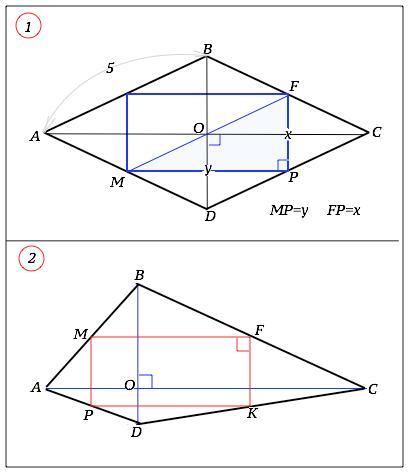
1) У ромбі ABCD точки F, P i M - середини сторін BC, CD, i AD відповідно. Знайдіть суму довжин діагоналей ромба, якщо АВ = 5 см, а периметр трикутника FPM дорівнює 12 см.
2) У чотирикутнику ABCD діагоналі AC i BD перпендикулярні. Точки M, F, K i P - середини сторін АВ, BC i DA відповідно. Доведіть, що MK = FP.
Ответы
1) В ромбе ABCD точки F, P и M – середины сторон BC, CD, и AD соответственно. Найдите сумму длин диагоналей ромба, если АВ = 5 см, а периметр треугольника FPM равен 12 см.
————
Диагонали ромба взаимно перпендикулярны и точкой пересечения делятся пополам.
Так как точки F, P и M – середины сторон BC, CD и AD, отрезок FP — средняя линия ∆ BCD и равна половине диагонали ВD; МР - средняя линия ∆ АСD и равна половие диагонали АС.
FP║BD; MP║AC; a так как АС⊥ВD, то FP⊥МР. ⇒ ∆ MFP – прямоугольный.
Ромб - параллелограмм, все стороны ромба равны. Поэтому равны и их половины. BF=AM, ВF и АМ параллельны⇒
АВFM - параллелограмм, MF=AB=5 см.
Периметр ∆ MFP=5+FP+MP=12 (см) ⇒ FP+MP=12-5=7 (см)
Диагонали ромба вдвое больше катетов ∆ MFP, ⇒
BD+AC=2•( FP+MP)=2•7=14 (см).
—————
2) В четырехугольнике ABCD диагонали AC и BD перпендикулярны. Точки M, F, K и P – середины сторон АВ, BC, СD и DA соответственно. Докажите, что MK = FP.
Точки M, F, K и P – середины сторон четырехугольника ABCD, поэтому являются средними линиями треугольников АВС, ВСD, АСD и АВD. По свойству средней линии треугольника:
МР=FK и параллельны BD, а MF=P и параллельны АС.
АС⊥BD , ⇒ соседние стороны четырехугольника PMFK , которые им параллельны, взаимно перпендикулярны. PMFK - прямоугольник, МК и PF его диагонали. Диагонали прямоугольника равны. MK и FP – его диагонали. ⇒ MK = FP