Предмет: Алгебра,
автор: Djdjdhfh
помогиииииииииииттттттттттттте пожалуйста
Приложения:

Ответы
Автор ответа:
2
Ответ:
Reshen
Объяснение:
Приложения:
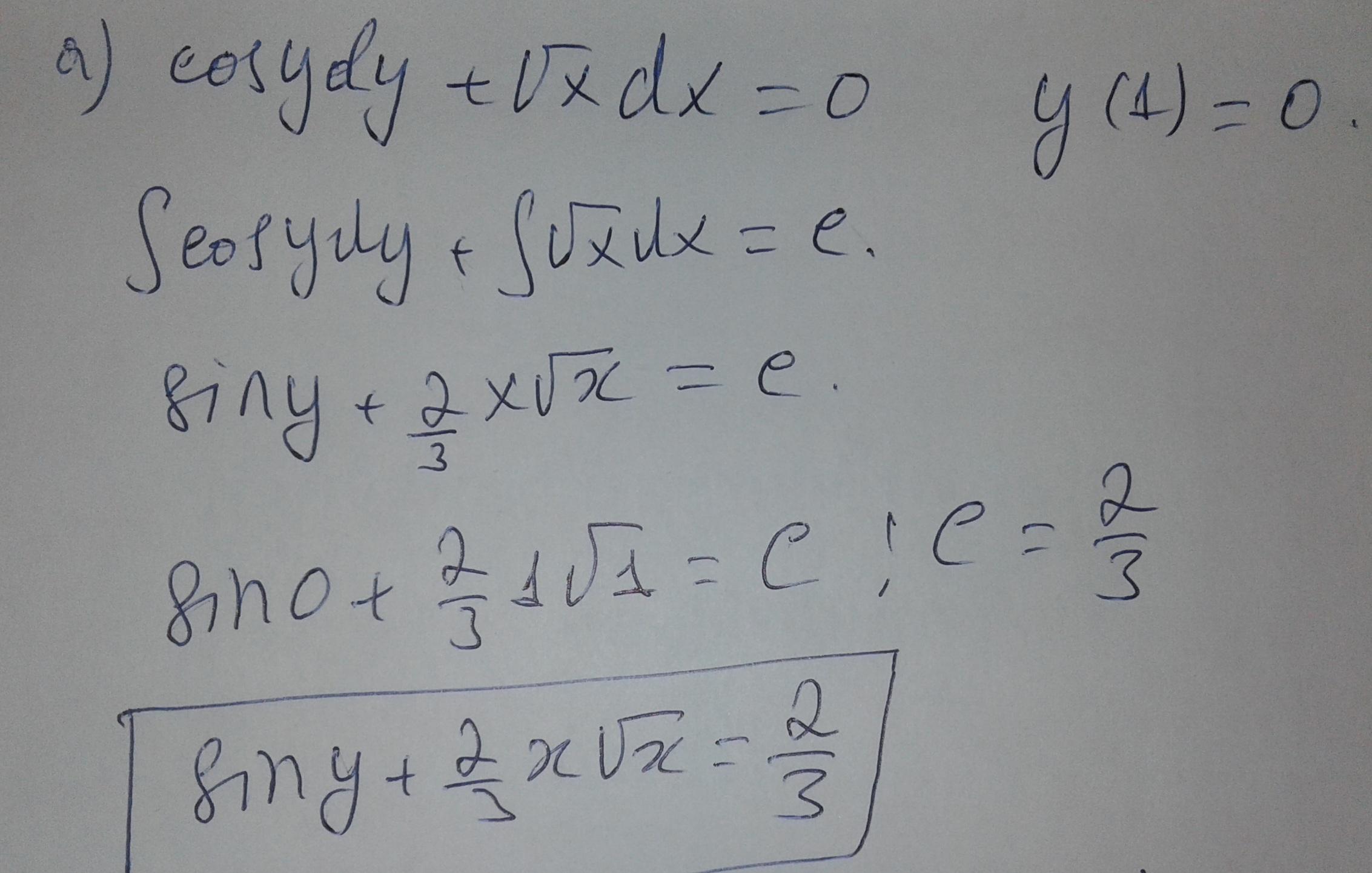
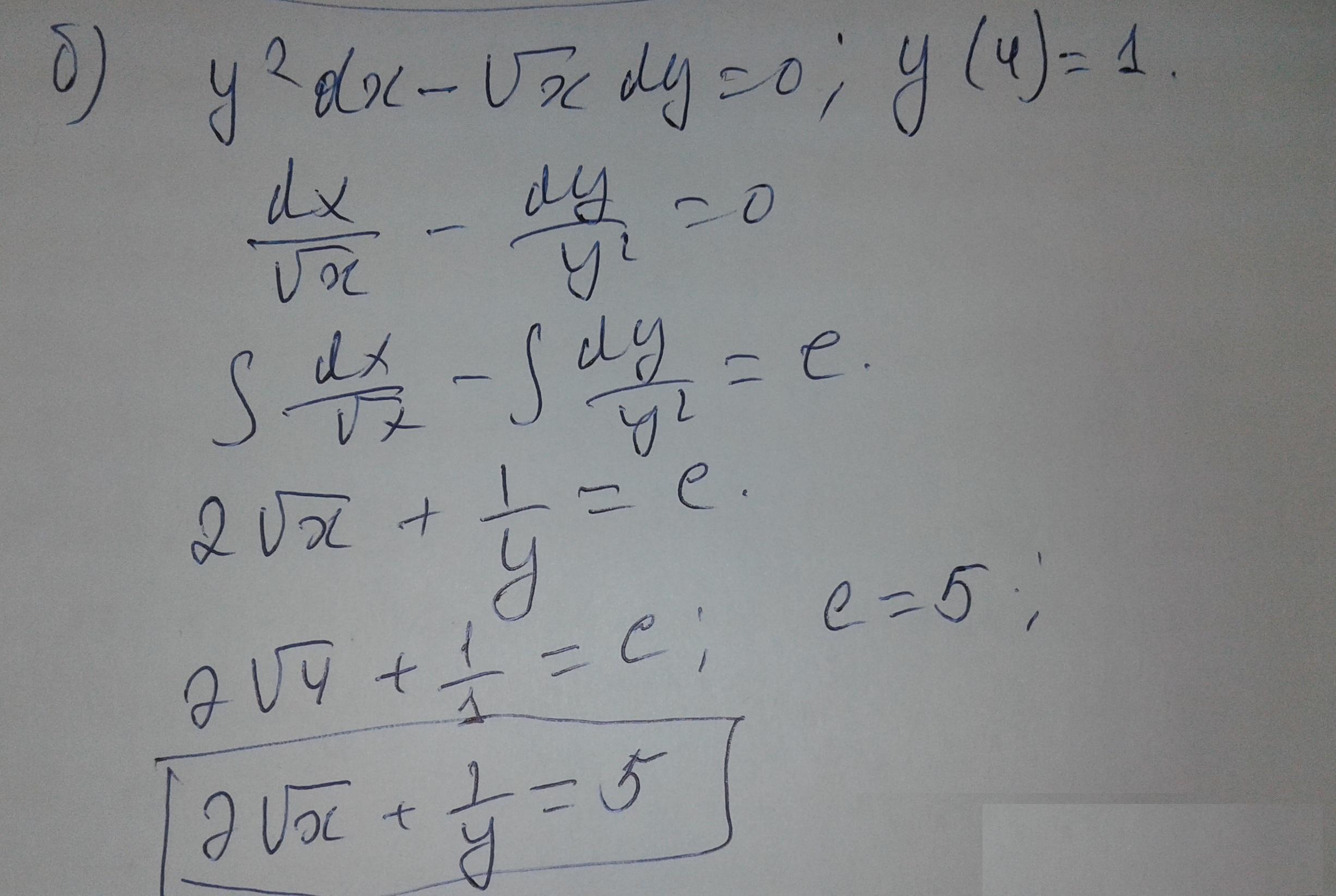
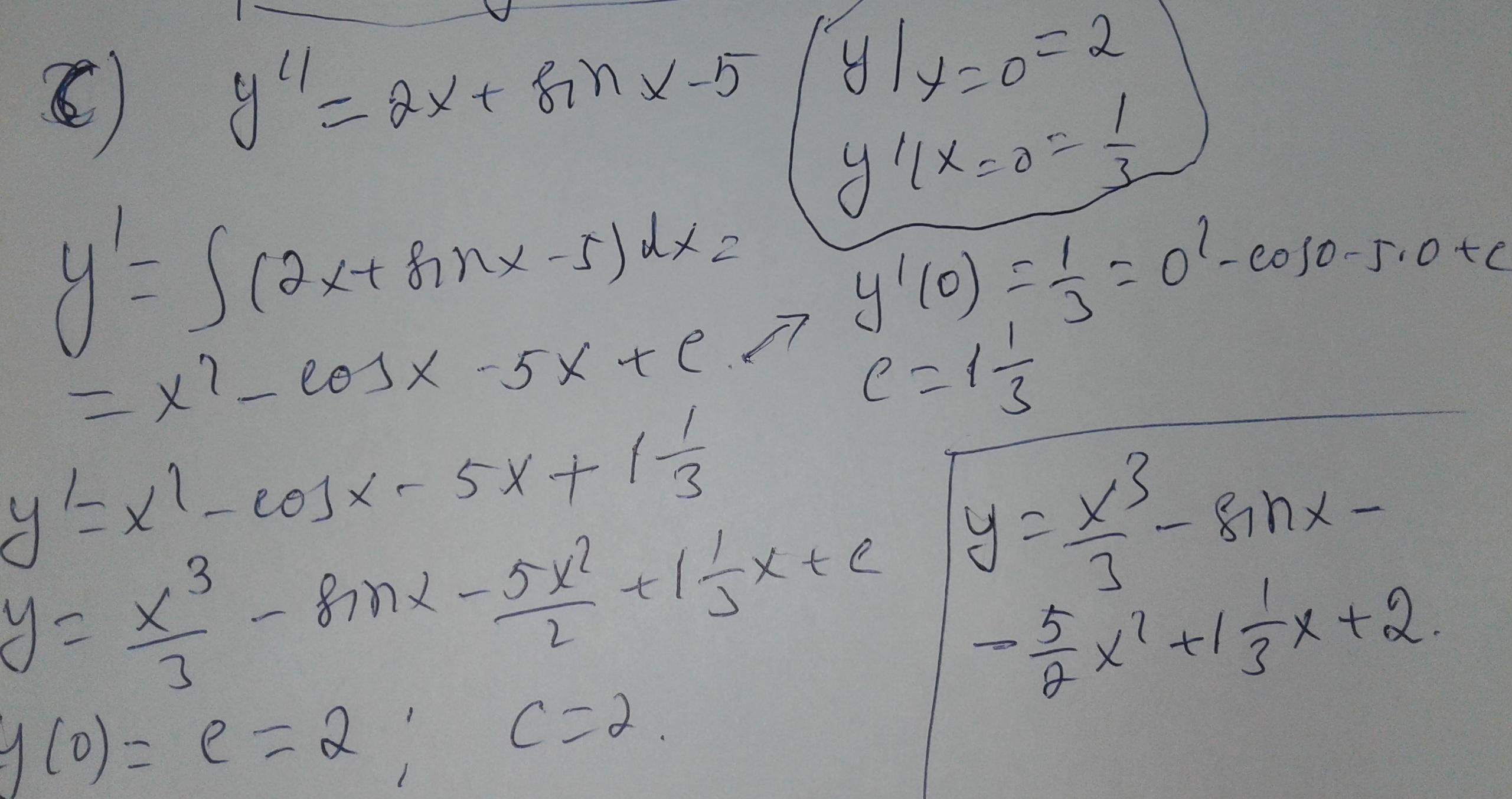
Автор ответа:
0
Ответ:
Похожие вопросы
Предмет: Русский язык,
автор: valikas2011
Предмет: Окружающий мир,
автор: Аноним
Предмет: Русский язык,
автор: АннаПавленкоОл
Предмет: Математика,
автор: Аноним
Предмет: Физика,
автор: babeor22p863sy