Предмет: Математика,
автор: denisnigmatullin017
решите пж
не могу пожалуйста
Приложения:
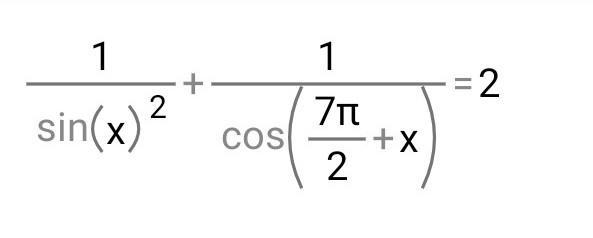
Guerrino:
воспользуйся тем, что минимальное значение левой части равно 2 (кстати, почему?)
а, косинус без квадрата... тогда не всегда так
1/sin^2x+1/sinx=2, 1/sinx=t;t^2+t=2;t=1;1/sinx=1;sinx=1;x=pi/2+2pik
там в ответе ещё есть точка 13 pi/6
Ответы
Автор ответа:
2
Ответ:
блин в ответе там ещё и 13pi/6
ответы в тригонометрических уравнениях могут не совпадать по форме, так как один ответ можно преобразовать к другому, но сути это не меняет . Можно вместо П/6+2Пm написать 13П/6+2Пm , так как это равенство будет описывать одни и те же углы ... Но всегда стараются взять углы поменьше ...Может, у тебя ещё какое-то условие к уравнению написано, что надо искать углы, принадлежащие какому-то промежутку ? Например, угол 13П/6 Є [2П;5П/2 ] .
Похожие вопросы
Предмет: Русский язык,
автор: азбука8
Предмет: Русский язык,
автор: yulvolk
Предмет: Английский язык,
автор: karina1488o
Предмет: Геометрия,
автор: 620veko320
Предмет: Математика,
автор: romansafigin2008