Предмет: Алгебра,
автор: raleksandrovic619
найти Sin π/3-a если cos a=13/12, 3π/2<a<2π
Приложения:
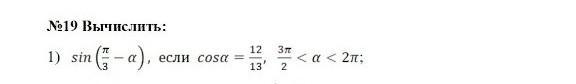
Ответы
Автор ответа:
0
Ответ:
Объяснение:
- Наш угол α лежит в 4 четверти => значение синуса в этой четверти будет отрицательным
Найдём sin α с помощью основного тригонометрического тождества:
Подставим:
Теперь по формуле синуса разности найдëм значение:
Подставим:
Похожие вопросы
Предмет: Технология,
автор: viktoriavtvtv678
Предмет: Русский язык,
автор: 1класс14
Предмет: Русский язык,
автор: DANILOKONIAK
Предмет: Математика,
автор: chelovek8519
Предмет: Алгебра,
автор: KingArslan