Предмет: Математика,
автор: mrx141203
y = 1+x^2 \ 1-x^2
Найти производную функции
Обьясните как вы решили!
Ответы
Автор ответа:
1
надеюсь понятно?????????
Приложения:
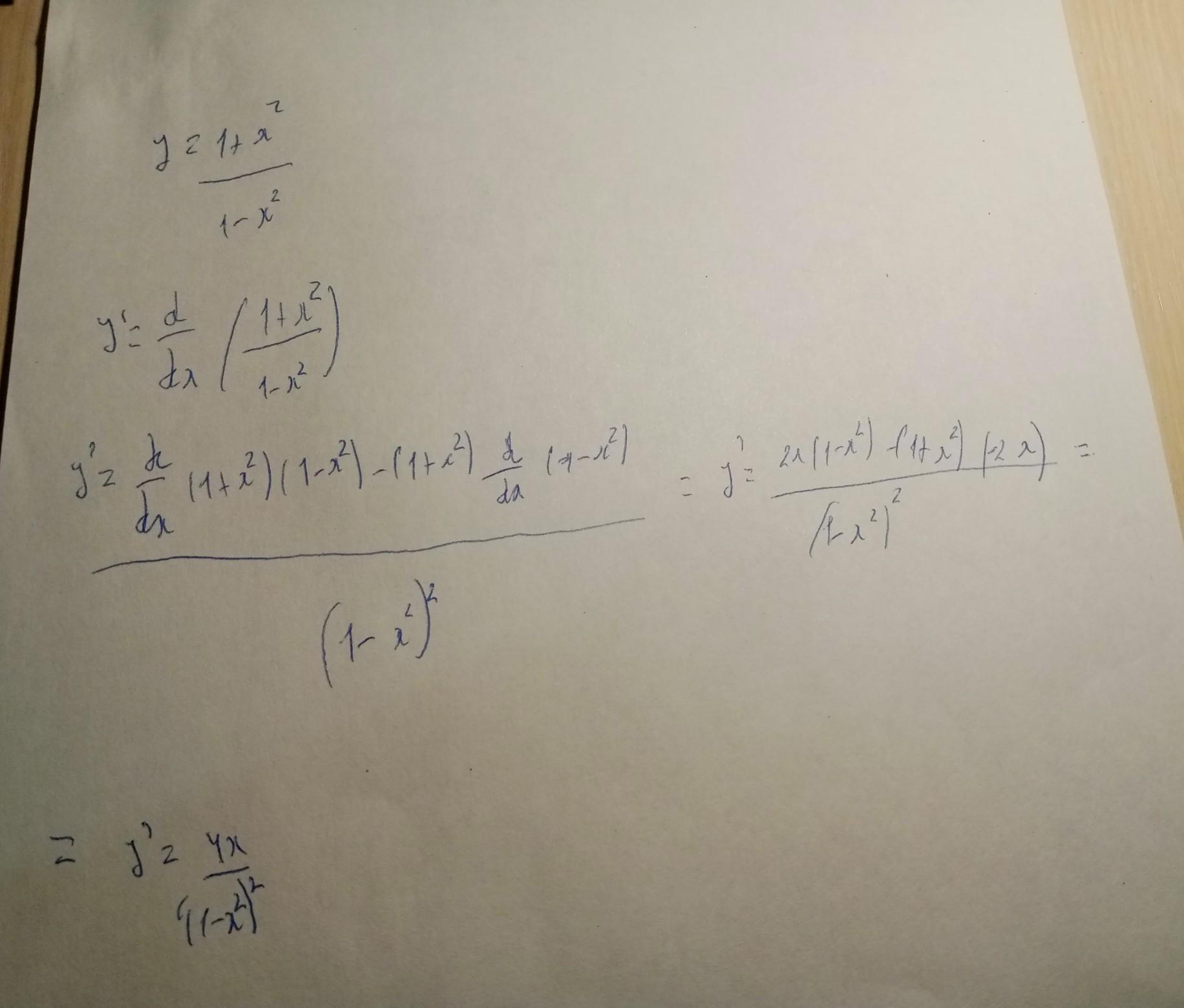
Автор ответа:
1
Ответ:
Пошаговое объяснение:
тут можно сразу находить производную
теперь
,с - любое число
(cx)'=c*x'
вроде всё
Похожие вопросы
Предмет: Английский язык,
автор: Аноним
Предмет: Русский язык,
автор: denikzenik228
Предмет: Английский язык,
автор: 79534476124
Предмет: Математика,
автор: iamevg123
Предмет: Українська мова,
автор: anuta110310