Question

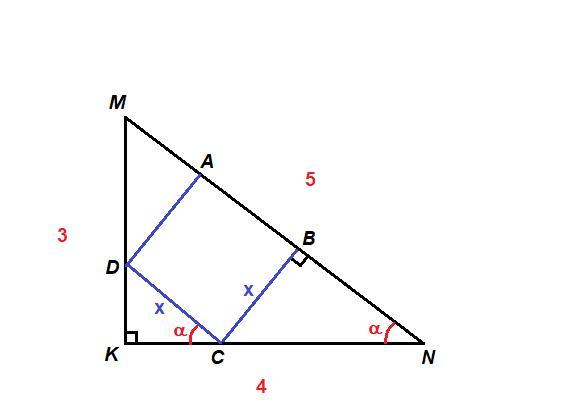
Вася верно нашёл и представил в виде несократимой дроби площадь квадрата ABCD, у которого вершины A и B лежат на стороне MN=5, C – на стороне NK=4, D – на стороне KM=3 треугольника KNM. Укажите числитель полученной Васей несократимой дроби.

Answer 1

Ответ:

3600

Объяснение:

Треугольник MNK со сторонами 3, 4 и 5 - египетский, прямоугольный.

ΔMNK:

$\sin\alpha =\dfrac{MK}{MN}=\dfrac{3}{5}=0,6$

$\cos\alpha =\dfrac{KN}{MN}=\dfrac{4}{5}=0,8$

Из прямоугольного треугольника BCN:

$\sin\alpha =\dfrac{CB}{CN}$

$CN=\dfrac{CB}{\sin\alpha}=\dfrac{x}{0,6}$

DC║AB, как противоположные стороны квадрата.

∠DCK = ∠BNC = α как соответственные при пересечении параллельных прямых DC и АВ секущей KN.

Из прямоугольного треугольника DKC:

$\cos\alpha =\dfrac{KC}{DC}$

$KC=DC\cdot \cos \alpha=0,8x$

KC + CN = KN = 4

$\dfrac{x}{0,6}+0,8x=4\; \: \; \: |\cdot 0,6$

$x+0,48x=2,4$

$1,48x=2,4$

$x=\dfrac{2,4}{1,48}=\dfrac{240}{148}=\dfrac{60}{37}$

Площадь квадрата:

$S=x^2=\left(\dfrac{60}{37}\right)^2$

$S=\dfrac{3600}{1369}$