Предмет: Математика,
автор: ghfghfghfg18
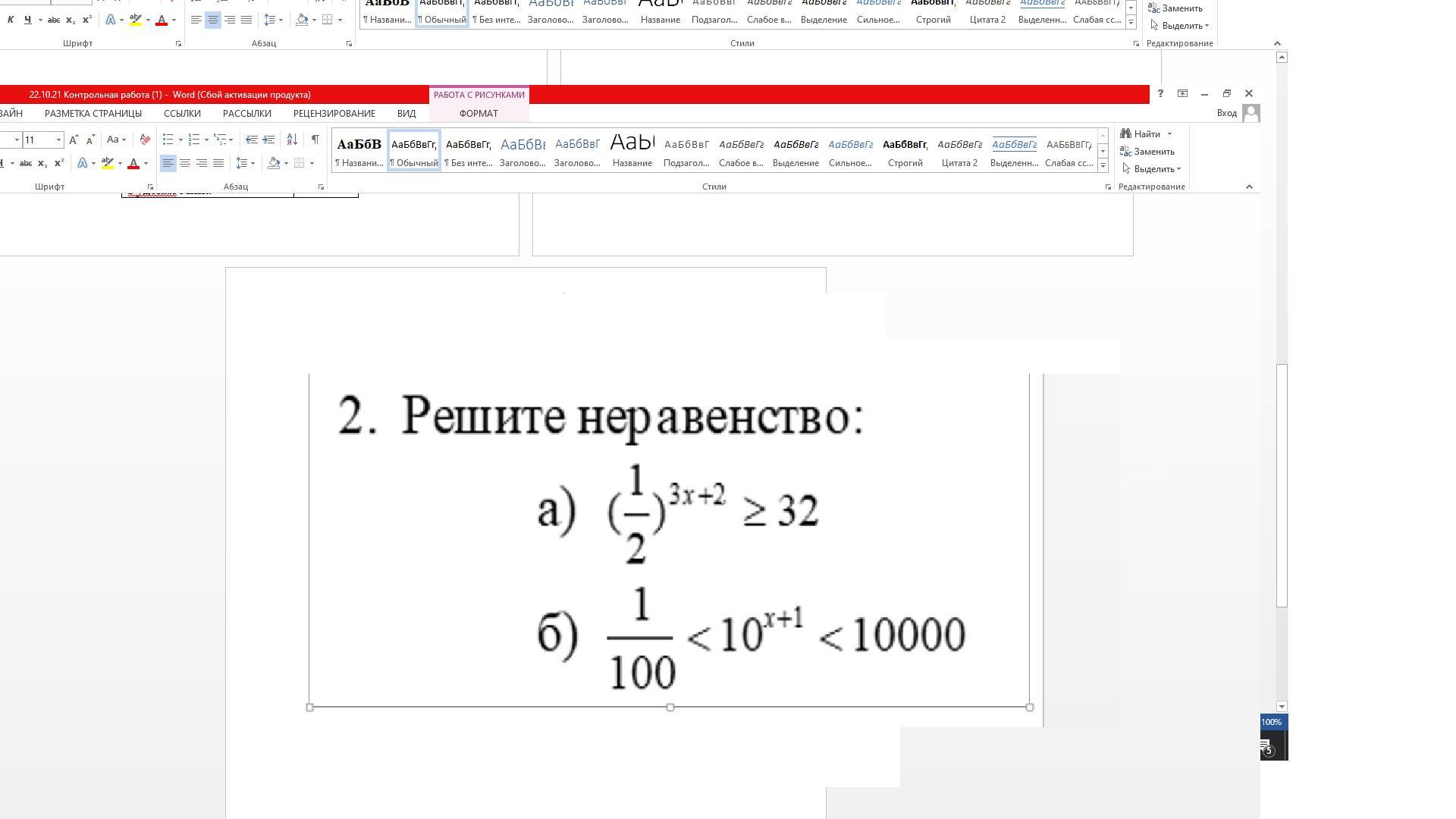
Решить 2 неравенства 40 БАЛЛОВ
Приложения:
Ответы
Автор ответа:
1
Ответ:
а).
б). -3<х<3
Пошаговое объяснение:
а).
основание степени а=(1/2)
0<(1/2)<1, => знак неравенства меняем
б).
основание степени а=10, 10>1, => знак неравенства не меняем
-2<х+1<4
-3<х<3
Похожие вопросы
Предмет: Русский язык,
автор: Ekat1999
Предмет: Русский язык,
автор: akihiko99
Предмет: Немецкий язык,
автор: kvest501
Предмет: Алгебра,
автор: amfelmat
Предмет: Русский язык,
автор: ususuvil