Предмет: Алгебра,
автор: popidans
помогите пожалуйста
Приложения:

Ответы
Автор ответа:
1
2. Выполните действия:
а)
б)
в)
3. Выполните действия:
а)
б)
4. Упростите выражение:
а)
б)
1. Упростить выражение:
а)
б)
в) на фото
Приложения:
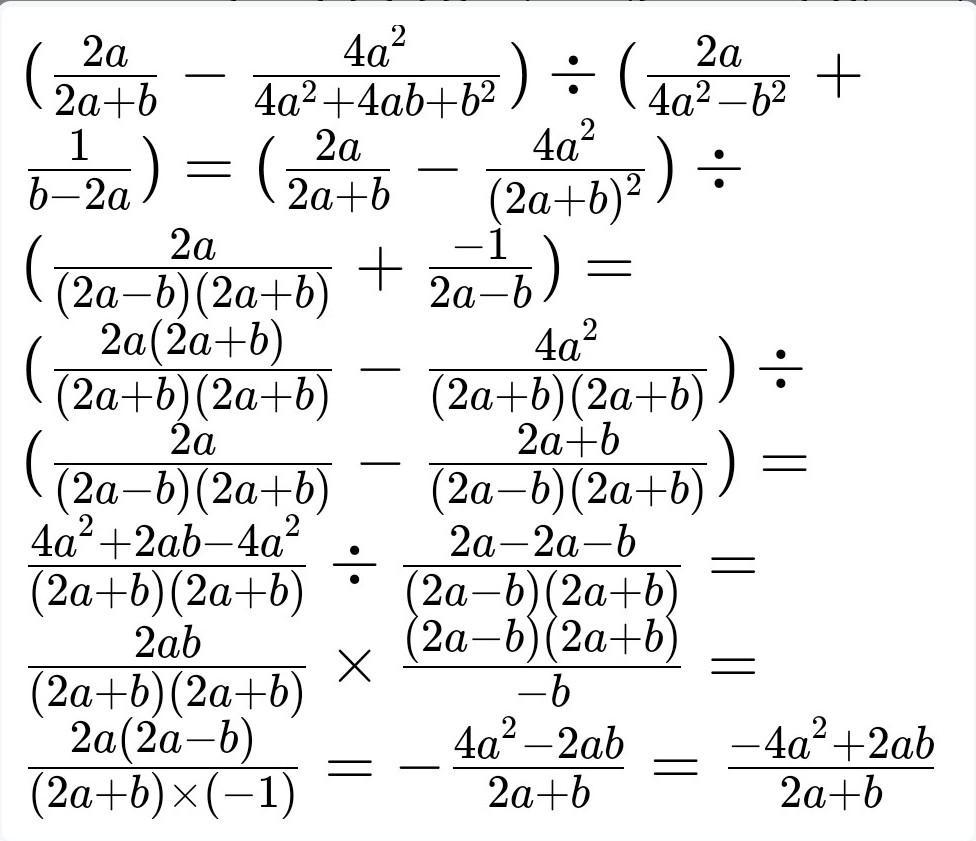
Похожие вопросы
Предмет: Қазақ тiлi,
автор: саида101
Предмет: Русский язык,
автор: 11112008
Предмет: Русский язык,
автор: 56562щ56275627
Предмет: Математика,
автор: sayana2002
Предмет: Биология,
автор: nike22052001