Предмет: Алгебра,
автор: artemtop574
помогите пожалуйста прошу вас
Приложения:
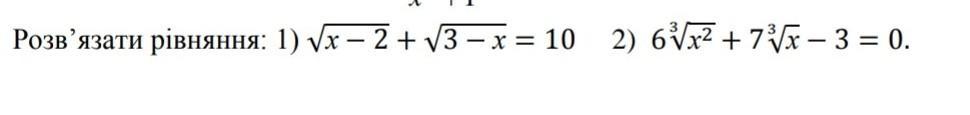
Universalka:
По моему в первом задании опечатка
а как правильно
Справа должно быть какое -то число но не 10 .
Возможно там не 10 , а 1 .
Второе легко решается заменой
Ответы
Автор ответа:
0
Ответ:
Объяснение:
Найдём ОДЗ:
На отрезке [2; 3]:
Тогда их сумма не превзойдёт 2, а 2 < 10, следовательно решений у уравнения не будет.
* К такому же выводу можно прийти, возводя левую и правую части уравнения в квадрат.
Ответ: ∅
Сделаем замену ∛x = t:
Обратная замена:
Ответ: -27/8; 1/27.
Автор ответа:
0
Ответ:
Объяснение:
N°1:
- Сделаем замену:
Тогда:
Подставляем:
При этом учитываем ОДЗ:
Продолжаем решать:
Корней в данном уравнении нет
N°2:
Сделаем замену:
Подставляем:
Теперь делаем обратную замену:
Похожие вопросы
Предмет: Другие предметы,
автор: ИЗО11
Предмет: Қазақ тiлi,
автор: nick104
Предмет: Английский язык,
автор: KJKJKJtyuikjmnb
Предмет: Химия,
автор: kolya20012607
Предмет: История,
автор: Поадр