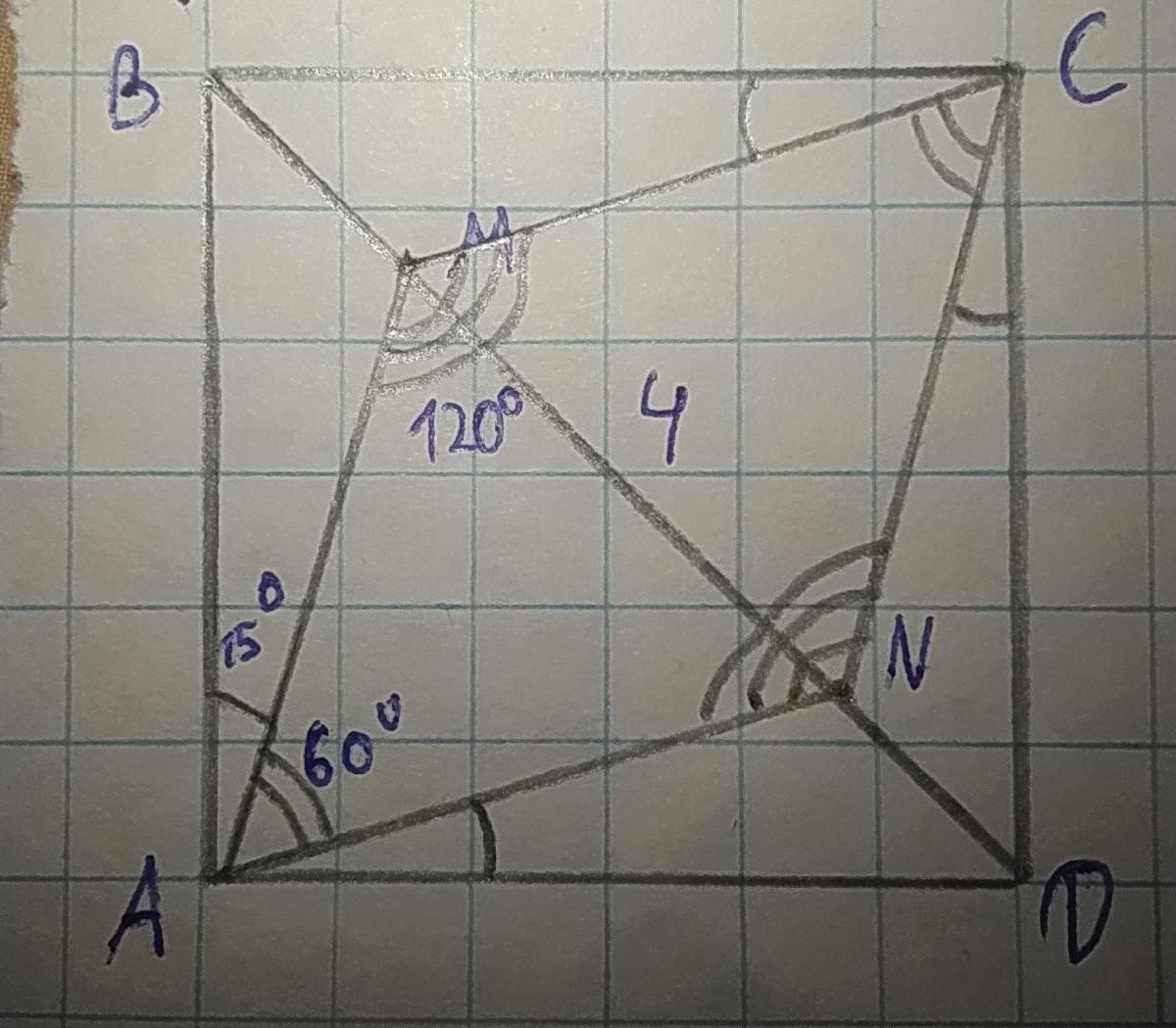
На диагонали BD квадрата ABCD взяты точки M и H такие, что BM=DN . Докажите что AMCN - ромб . Найдите его периметр, если MN=4 см и угол BAM =15°
Ответы
В квадрате ABCD, A - прямой угол(90°).
Углы BAM и NAD одинаковы(по 15°).
Тогда угол MAN = угол A - угол BAM - угол NAD = 60°.
BM = DN
Треугольники ABM с CBM и треугольники ADN с CDN имеют одинаковые углы(15°, 45°, 90°) и общие одинаковые стороны BM и ND соответственно.
Проведём диагональ AC. В квадрате диагонали при пересечении делятся пополам и образуют 4 угла по 90°.
Углы MAN и MCN равны и углы AMC с ANC равны.
Исходя из выше сказанного и того что ABCD - квадрат, можно утверждать что AMCN - ромб.
В ромбе AMCN, MN делит углы AMC и ANC пополам(по 60°).
Тогда треугольник AMN равносторонний (все стороны по 4 см).
P(AMCN) = 4 × a = 4 × 4 = 16(см).
Если увидели ошибку или хотите дополнить ответ, пишите в комментарии или в ЛС.
Ответ:
16 см
Могут быть допущены граматичиские ошибки, я просто с Украины))