Предмет: Математика,
автор: grizlixalk
Помогите срочно нада решть. Дам 100 балов
Приложения:
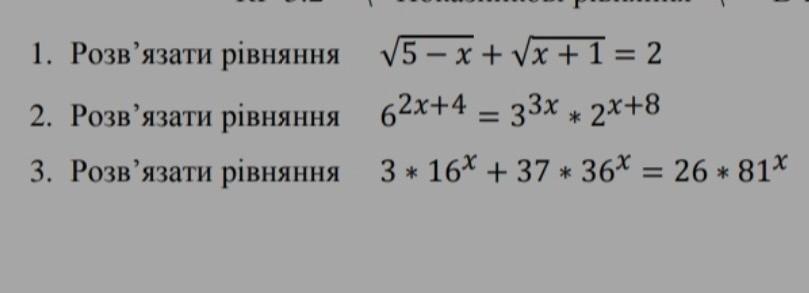
Ответы
Автор ответа:
1
Ответ:
1) x∈∅ 2) x = 4 3) x = 1/2
Пошаговое объяснение:
№1
ОДЗ:
x∈[-1;5]
Такие уравнения чаще всего решают методом подношения в квадрат, по скольку имеется квадратный корень. Но нужно знать условие подношения в квадрат. Если правая и левая часть уравнения не отрицательны, мы имеем право поднести в квадрат и это будет равносильный переход. Так и сделаем.
Корень по опредилению не отрицателен. Уравнение не имеет решения
x∈∅
№2
x = 4
Похожие вопросы
Предмет: Русский язык,
автор: almazero
Предмет: Қазақ тiлi,
автор: nattullka
Предмет: Русский язык,
автор: умняша131
Предмет: Алгебра,
автор: vanyushkinavik
Предмет: Математика,
автор: zhilyakova97