Предмет: Геометрия,
автор: ammaim1999
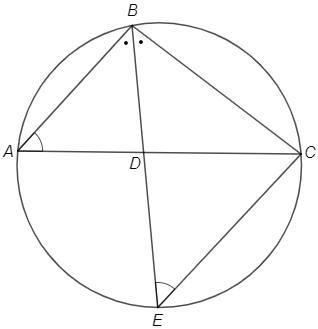
Биссектриса BD треугольника ABC продлена до пересечения с его описанной окружностью в точке E. Найдите DE, если AB = 4, BD = 3, BC = 5.
Ответы
Автор ответа:
2
∠BAC=∠BEC (вписанные углы, опирающиеся на одну дугу)
△BAD~△BEC (по двум углам)
AB/BE =BD/BC => 4/BE =3/5 => BE=20/3
DE =BE-BD =20/3 -3 =11/3
Приложения:
Автор ответа:
2
Ответ:
ед.
Объяснение:
Дано: ΔАВС;
BD - биссектриса;
АВ = 4; BD = 3; ВС = 5.
Найти: DE.
Решение:
Рассмотрим ΔABD и ΔЕВС.
∠1 = ∠2 (BD - биссектриса)
∠3 = ∠4 (вписанные, опираются на одну дугу)
⇒ ΔABD ~ ΔЕВС.
Составим пропорцию:
Пусть DЕ = х, ⇒ ВЕ = 3+х.
Приложения:

kosyksona:
ьдди
Похожие вопросы
Предмет: Русский язык,
автор: 1231546
Предмет: Русский язык,
автор: алинка168
Предмет: Английский язык,
автор: Treyla
Предмет: Английский язык,
автор: mariaatwogaman