Предмет: Алгебра,
автор: Аноним
завдання на фото
Срочно треба
Приложения:
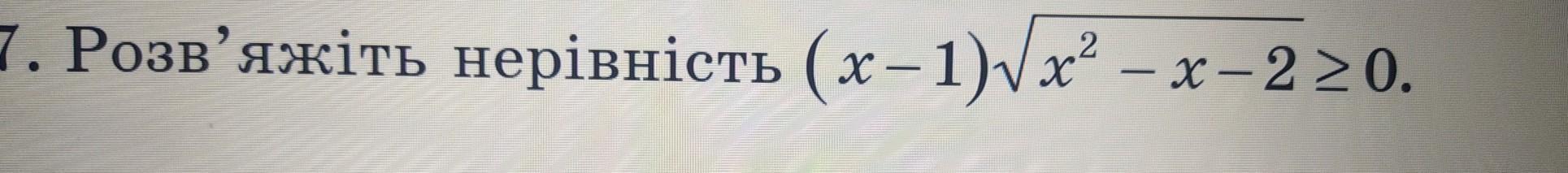
Ответы
Автор ответа:
1
Ответ:
x = - 1 или x ≥ 2
неравенство равносильно совокупности
решим уравнение совокупности
оно равносильно системе
неравенство совокупности равносильно системе
объединяем решения
O т в е т:
Похожие вопросы
Предмет: Окружающий мир,
автор: Аноним
Предмет: Русский язык,
автор: minecraft56russ
Предмет: Русский язык,
автор: vikor87
Предмет: Химия,
автор: Аноним
Предмет: Математика,
автор: Аноним