Question

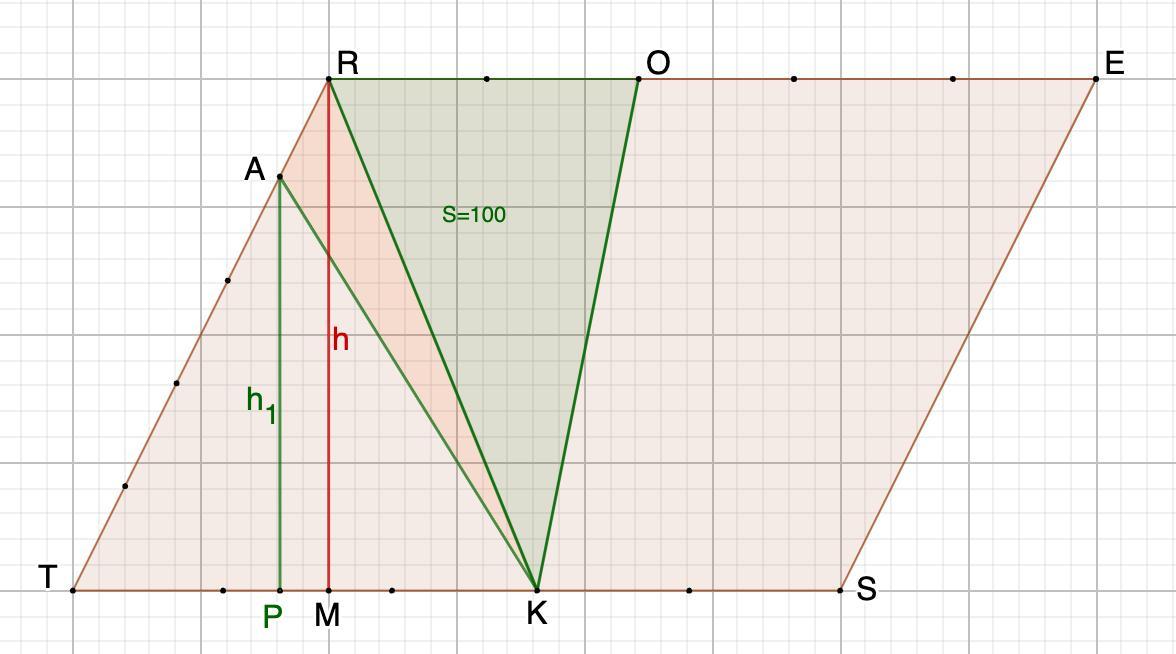
Точки T, R,E, S - последовательные вершины параллелограмма. На отрезке TS отмечена точка K такая, что TK:KS=3:2. На отрезке RE отмечена точка O такая, что RO:OE=2:3. На отрезке TR отмечена точка A такая, что TA:AR=4:1. Найдите площадь треугольника RAK, если площадь треугольника ROK равна 100.

Answer 1

Ответ:

30

Объяснение:

TS = RE = a

RO : OE = 2 : 3, значит

$RO=\dfrac{2}{5}RE=\dfrac{2}{5}a=0,4a$

TK : KS = 3 : 2, значит

$TK=\dfrac{3}{5}TS=\dfrac{3}{5}a=0,6a$

∠KRO = ∠RKT = α как накрест лежащие при пересечении параллельных прямых RE и TS секущей RK.

Площадь треугольника ROK:

$S_{ROK}=\dfrac{1}{2}RO\cdot RK\cdot \sin\alpha$

$S_{ROK}=\dfrac{1}{2}\cdot 0,4a\cdot RK\cdot \sin\alpha=0,2a\cdot RK\cdot \sin\alpha=100$

$a\cdot RK\cdot\sin\alpha=500$

Площадь треугольника RTK:

$S_{RTK}=\dfrac{1}{2}\cdot KT\cdot RK\cdot \sin\alpha$

$S_{RTK}=\dfrac{1}{2}0,6a\cdot RK\cdot \sin\alpha=0,3a\cdot RK\cdot \sin\alpha$

$S_{RTK}=0,3\cdot 500=150$

Площади треугольников с общей высотой относятся как стороны, к которым проведена высота.

В треугольниках RTK и RAK можно провести общую высоту из вершины К, значит

$\dfrac{S_{RAK}}{S_{RTK}}=\dfrac{RA}{RT}$

$\dfrac{S_{RAK}}{150}=\dfrac{1}{5}$

$\boldsymbol{S_{RAK}}=\dfrac{150}{5}\boldsymbol{=30}$

Answer 2

Ответ:

S (ΔRAK) = 30 ед².

Объяснение:

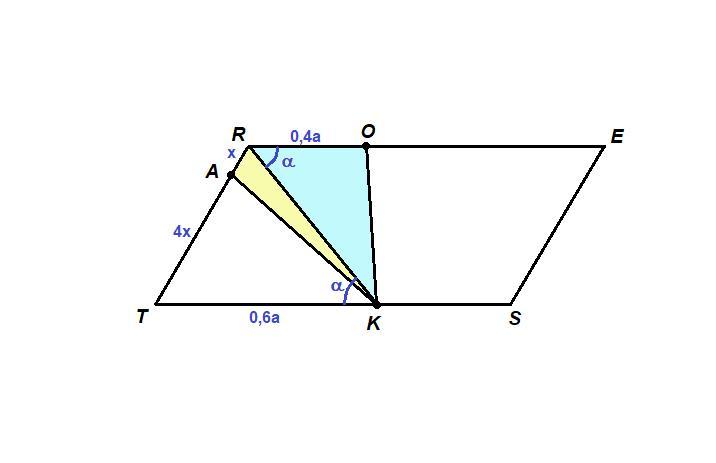
Дано: TRES - параллелограмм.

TK:KS=3:2; RO:OE=2:3; TA:AR=4:1;

S (ΔROK) = 100.

Найти: S (ΔRAK)

Решение:

1. Пусть ТК = 3х, тогда KS = 2x.

• Противоположные стороны параллелограмма равны.

⇒ RO = 2х; OE = 3х.

2. Рассмотрим ΔROK.

• Площадь треугольника равна половине произведения основания на высоту.

$\displaystyle S_{ROK}=\frac{1}{2}RO*RM\\\\100=\frac{1}{2} *2x*h\\\\h=\frac{100}{x}$

2. Рассмотрим ΔTRK.

$\displaystyle S_{TRK}=\frac{1}{2}TK*h = \frac{1}{2}*3x*\frac{100}{x}=150$

3. Рассмотрим ΔTAP и ΔTRM

• Если две прямые перпендикулярны третьей, то они параллельны между собой.

AP ⊥ TK; RM ⊥ TK ⇒ AP || RM

• Лемма. Если две стороны треугольника пересекает прямая, параллельная третьей стороне, то она отсекает треугольник, подобный данному.

⇒ ΔTAP ~ ΔTRM

Пусть AR = y; тогда ТА = 4у, ⇒TR = 5y.

$\displaystyle \frac{TA}{TR}=\frac{y_1}{h} \\\\\frac{4y}{5y} =\frac{h_1*x}{100} \\\\h_1=\frac{4*100}{5x} =\frac{80}{x}$

4. Найдем площадь ΔТАК:

$\displaystyle S_{TAK}=\frac{1}{2}TK*h_1=\frac{1}{2}*3x*\frac{80}{x}=120$

5. Найдем площадь ΔRAK:

$\displaystyle S_{RAK}=S_{TRK}-S_{TAK}=150-120=30$

S (ΔRAK) = 30 ед².