Предмет: Математика,
автор: maklinskijgerman
Решить уравнение: lg(x^2-6x+9)-2lg(x-7)=lg9
Приложения:
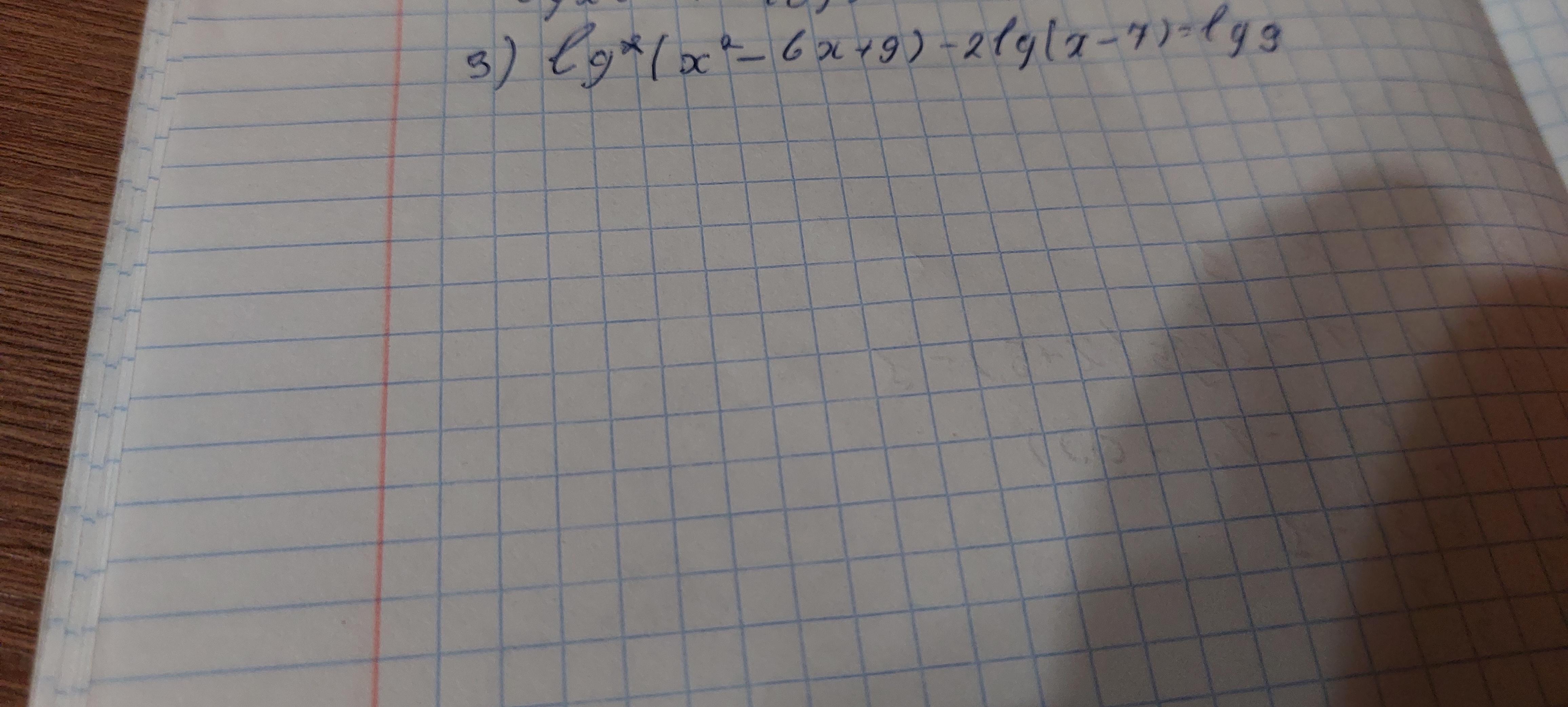
Ответы
Автор ответа:
1
Ответ:
9
Пошаговое объяснение:
ОДЗ:
Похожие вопросы
Предмет: Українська мова,
автор: Фике
Предмет: Русский язык,
автор: Даруна
Предмет: Русский язык,
автор: ощьщ56
Предмет: Русский язык,
автор: jundndjd
Предмет: Информатика,
автор: Defalt13