Предмет: Алгебра,
автор: modenov04
Решить уравнение СРОЧНО!!! 100 БАЛЛОВ. Уравнение на фото. Подробное решение.
Приложения:
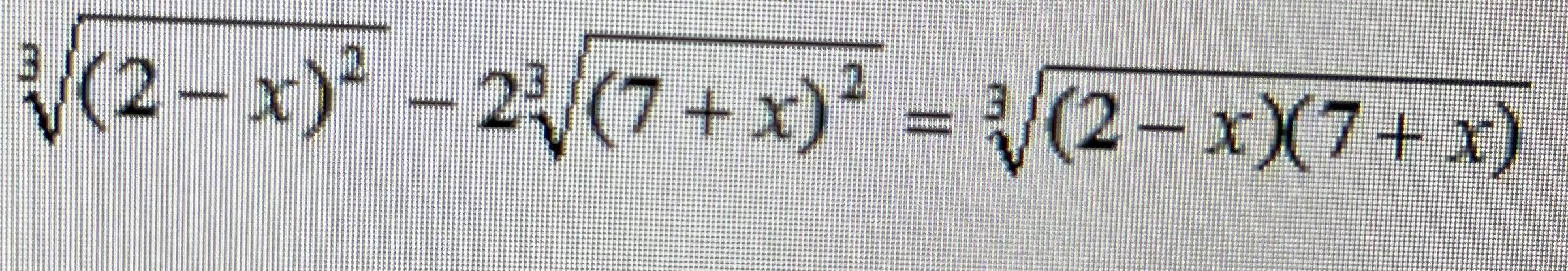
Ответы
Автор ответа:
1
Ответ:
Объяснение:
Решить уравнение
Решение.
Пусть Тогда
1)
2)
решений нет
О т в е т:
Похожие вопросы
Предмет: Английский язык,
автор: настень11
Предмет: Русский язык,
автор: DinaBendeliani
Предмет: Русский язык,
автор: nikidinroman
Предмет: Математика,
автор: 44080006961
Предмет: Русский язык,
автор: gm117634