Найти четыре первых отличных от нуля члена разложения в ряд Маклорена решения задачи Коши!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
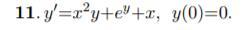
Ответы
Ответ: y≈x+x²+1/2*x³+2/3*x⁴.
Пошаговое объяснение:
Будем искать решение в виде y=y(0)+y'(0)*x/1!+y"(0)*x²/2!+... Задача состоит в нахождении значений первых четырёх значений y'(0), y"(0),..., отличных от нуля. Решение будем искать методом последовательного дифференцирования.
1) используя условие y(0)=0, из данного уравнения находим y'(0)=1.
2) дифференцируя данное уравнение, получаем уравнение y"=2*x*y+x²*y'+e^y*y'+1. Подставляя в него известные значения y(0) и y'(0), находим y"(0)=2.
3) дифференцируя уравнение для y", получаем уравнение y'''=2*y+4*x*y'+x²*y"+e^y*(y')²+e^y*y". Подставляя в него известные значения y(0), y'(0) и y"(0), находим y'''(0)=3.
4) дифференцируя уравнение для y''', получаем уравнение y''''=6*y'+6*x*y"+x²*y'''+e^y*(y')³+3*e^y*y'*y"+e^y*y'''. Подставляя в него известные значения y(0), y'(0), y"(0) и y'''(0), находим y''''(0)=16. Таким образом, y'(0), y"(0), y'''(0) и y''''(0) отличны от нуля, а потому y≈x+x²+1/2*x³+2/3*x⁴.