Предмет: Алгебра,
автор: atakhanova0408
помогитеееееее пжжжжжжж
Приложения:

Elena3982:
Слишком много расписывать.Устроит только ответ?
но мне надо с решением
Там на целую страницу.
да знаю, из-за этого не могу решить
пожалуйста помогите
Подожди тогда.Много писать.
Ответы
Автор ответа:
1
Объяснение:
Вот тебе ответ.........
Приложения:
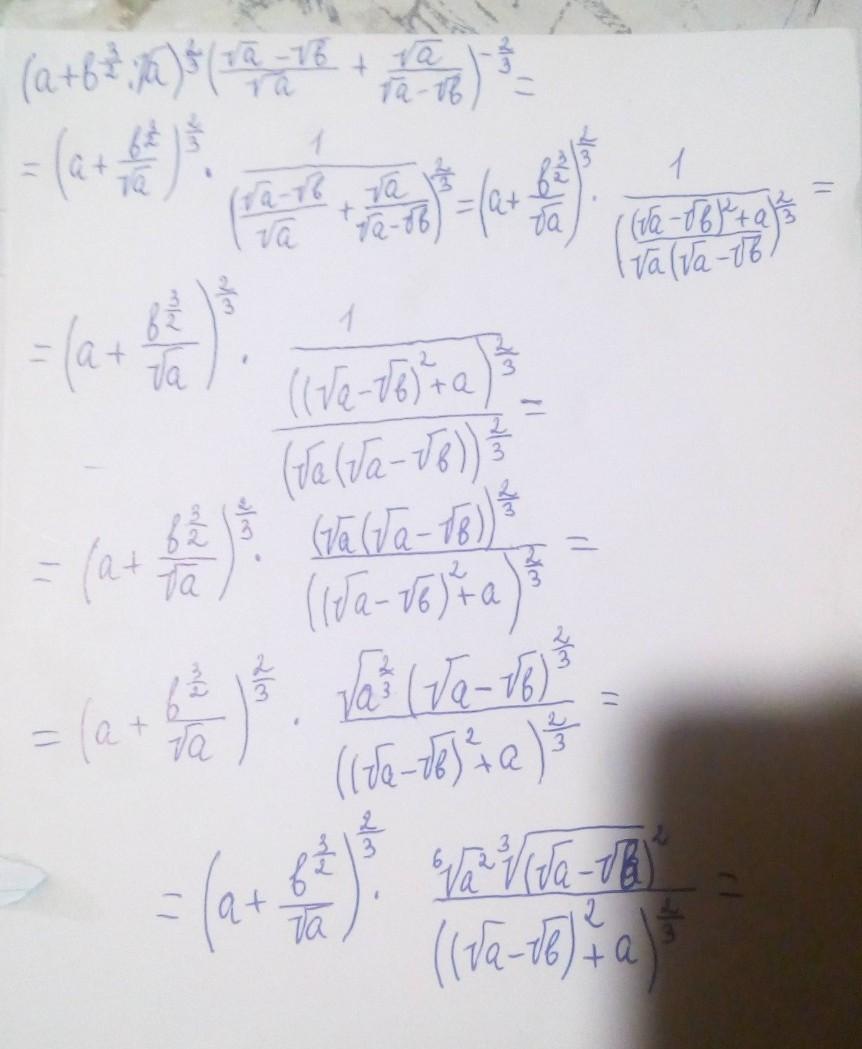
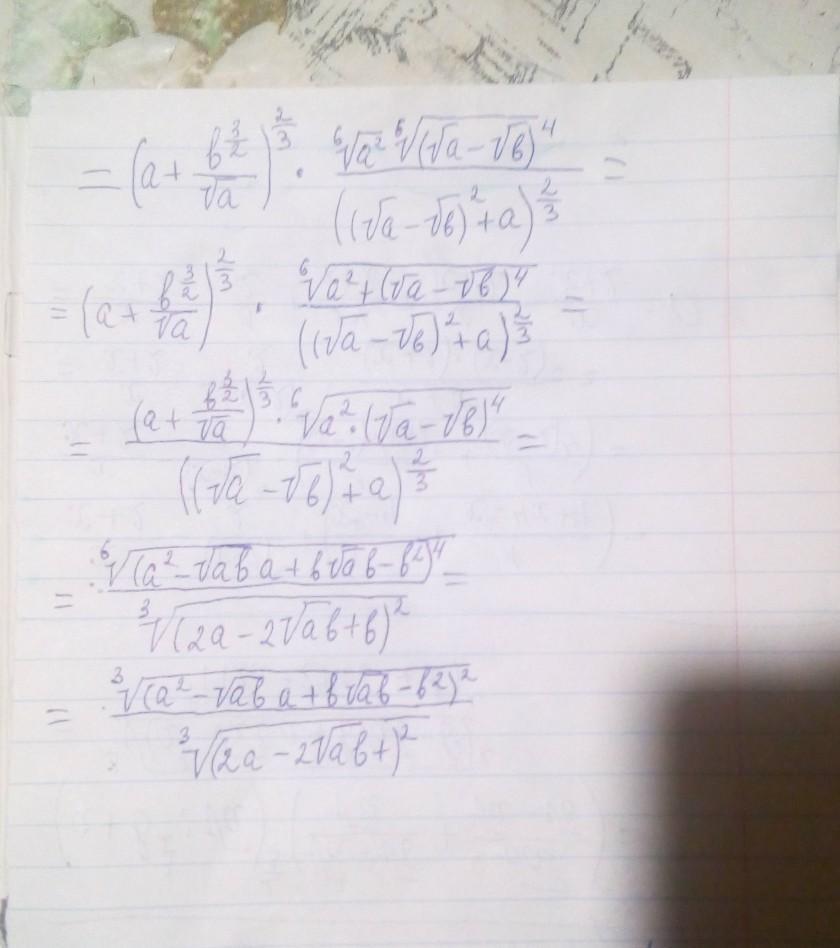
Автор ответа:
1
Ответ:
Приложения:
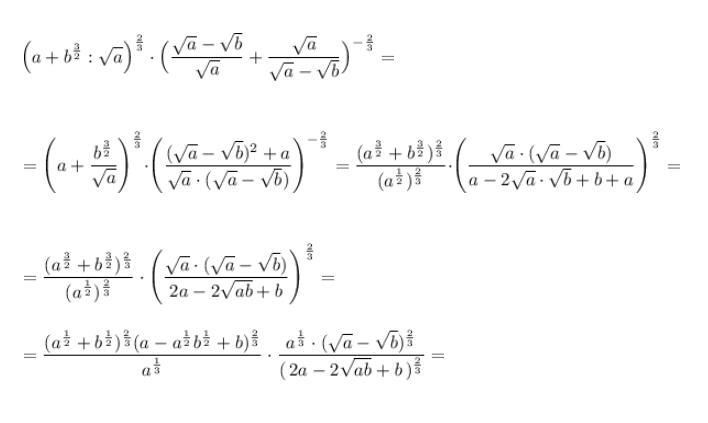
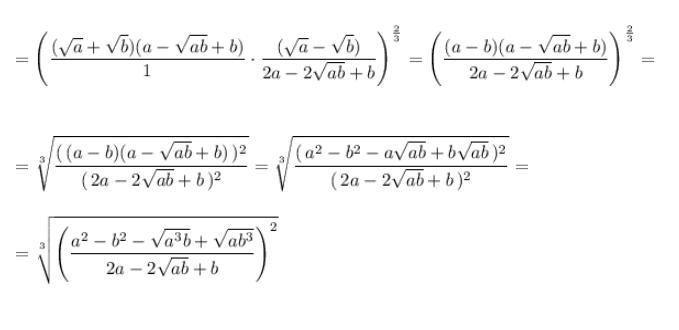
Похожие вопросы
Предмет: Русский язык,
автор: adilnoorijan
Предмет: Окружающий мир,
автор: vddyjfx
Предмет: Українська мова,
автор: Аноним
Предмет: Физика,
автор: Аноним
Предмет: Экономика,
автор: anjela131402