Question

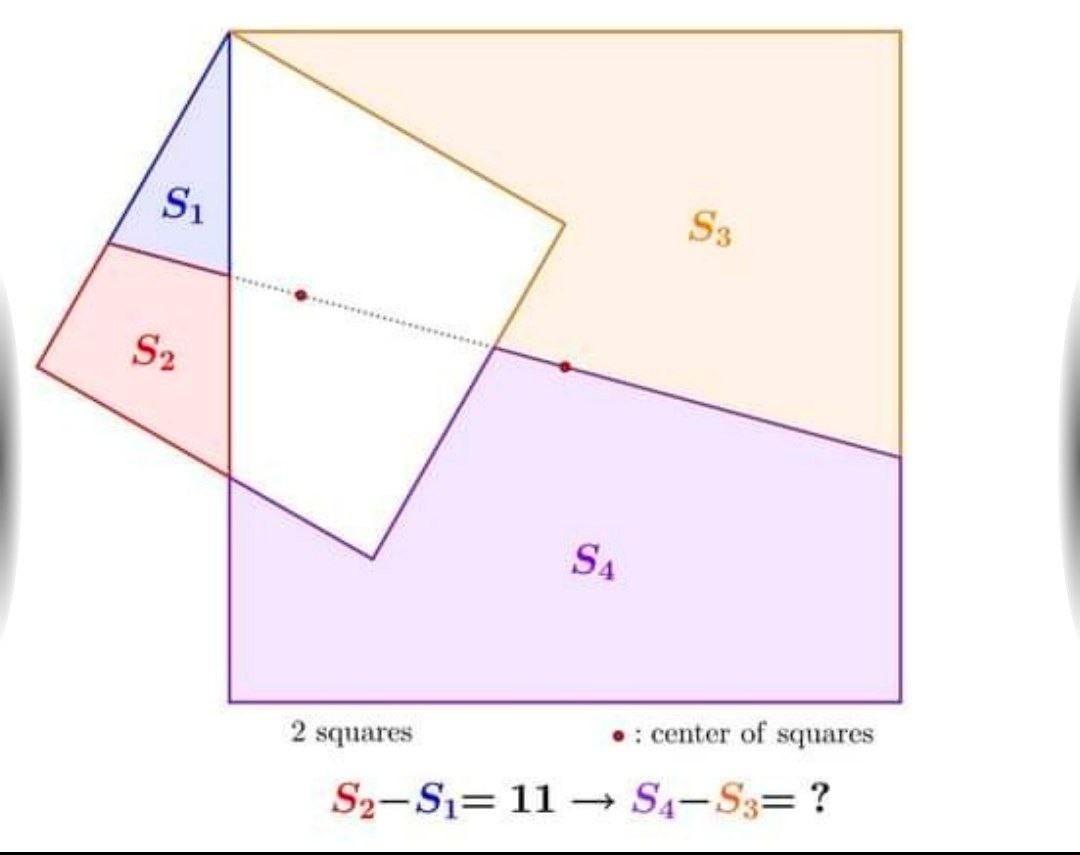
Квадрат.Попробуйте найти S4-S3,если S2-S1=11​

Answer 1

Ответ:

11

Объяснение:

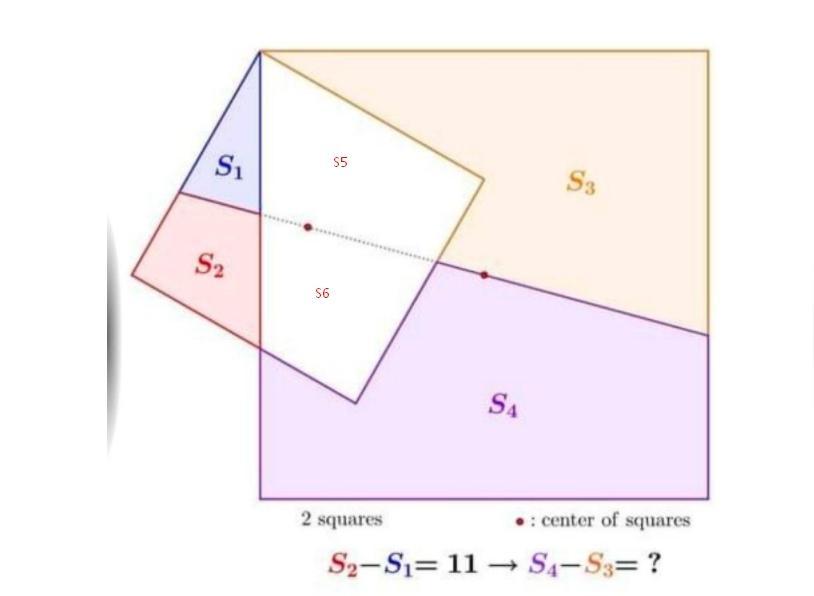
прямая проходящая через центр квадрата делит квадрат на две части с равными площадями.

в малом квадрате S2+S6=S1+S5

в большом квадрате S4+S6=S3+S5

где S6 - белая фигура в нижней части

где S5 - белая фигура в верхней части

S2+S6=S1+S5 => S6-S5=S1 - S2

S4+S6=S3+S5 => S6-S5=S3- S4

отсюда

S1 - S2 = S3- S4

значит S4 - S3 = S2 - S1 = 11 - это ответ