Предмет: Алгебра,
автор: leravasilati
Решить иррациональное уравнение. 10 класс
Приложения:
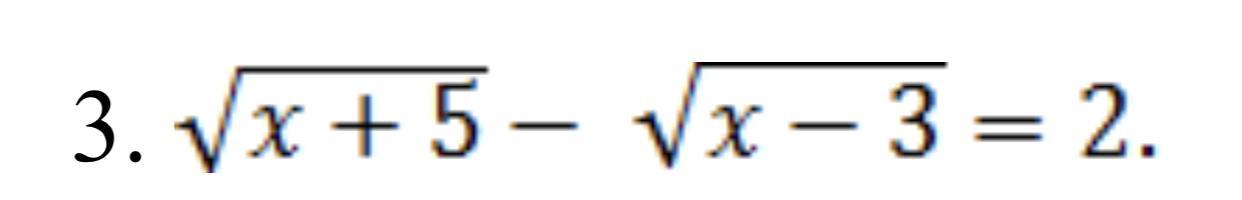
Ответы
Автор ответа:
0
Ответ:
Объяснение:
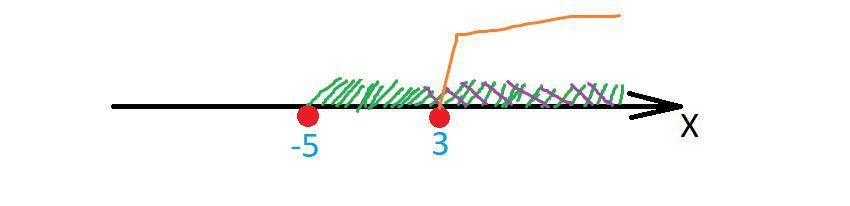
ОДЗ:
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: kotikmi
Предмет: Қазақ тiлi,
автор: кеп16
Предмет: Русский язык,
автор: стас114
Предмет: Литература,
автор: SafronovStepan
Предмет: Физика,
автор: giperbon