помогите решить пожалуйста
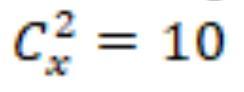

Ответы
Відповідь:
Покрокове пояснення:
С(2,х)=х!/(2!(х-2)!)=10
х!/(х-2)!=20
х(х-1)=20
х²-х-20=0
х=(1±(1+80)^½)/2=(1±9)/2
х1=5, х2=-4, но х>0
Ответ х=5
А(2,х)=182
А(2,х)=х!/(х-2)!
х(х-1)=182
х²-х-182=0
х=(1±(1+728)^½)/2=(1±27)/2
х1=14, х2=-13
Второй корень отбрасывает как отрицательное значение
Ответ х=14
Теория:
Решение:
1)
ОДЗ: х≥0, т.к. факториал определен только для целых неотрицательных чисел
Произведение равно нулю когда один или оба множителя равны нулю
а)
Результатом факториала может являться только целое положительное число, так что здесь решений нет
б)
- не подходит по ОДЗ
Ответ: х=5
2)
Произведение равно нулю когда один или оба множителя равны нулю
а)
Результатом факториала может являться только целое положительное число, так что здесь решений нет
б)
- не подходит по ОДЗ
Ответ: х=14