Предмет: Геометрия,
автор: nara62375
Два кути паралелограма відносять як 3:7. Знайти кут між висотами паралелограма проведеними з вершини тупого кута!?.
Ответы
Автор ответа:
2
Ответ:
54°
Объяснение:
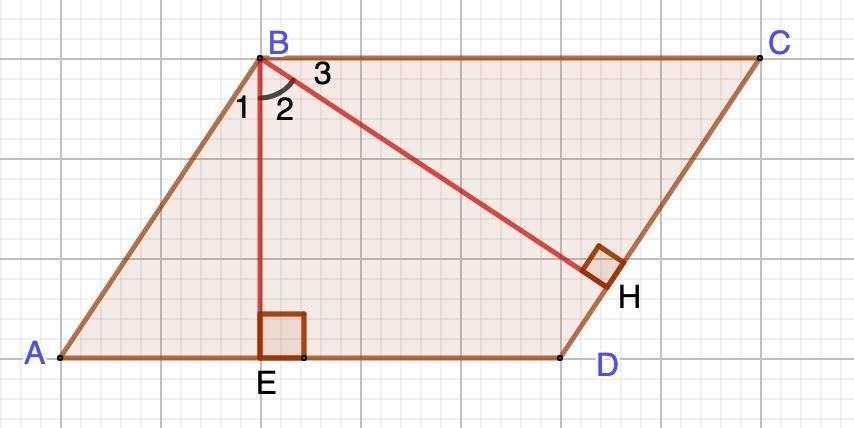
Дано: ABCD - параллелограмм.
∠А:∠В=3:7
ВЕ и ВН - высоты
Найти: ∠2
Решение:
1. Найдем углы параллелограмма.
- Углы, прилежащие к одной стороне параллелограмма в сумме равны 180°.
Пусть ∠А=3х, тогда ∠В=7х.
Составим уравнение:
3х+7х=180°
10х=180°
х=18°
⇒ ∠А=3х=54°; ∠В=7х=126°
- Противоположные углы параллелограмма равны.
∠А=∠С=54°
∠В=∠D=126°
2. Рассмотрим ΔАВЕ - прямоугольный.
- Сумма острых углов прямоугольного треугольника равна 90°.
⇒ ∠1=90°-∠А=90°-54°=36°
3. Рассмотрим ΔВСН - прямоугольный.
∠3=90°-∠С=90°-54°=36°
4. ∠2=∠В-(∠1+∠3)=126°-(36°+36°)=54°
Ответ: 54°
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: gulnazmoldabaeva
Предмет: Русский язык,
автор: timurlyadnev
Предмет: Русский язык,
автор: 109876543212
Предмет: Математика,
автор: EvaKissss
Предмет: Математика,
автор: ooxxxxaaaannnnaaaa