Question

пожалуйста помогите решить задачу: Докажите,что если катер прямоугольника треугольника равен половине гипотенузу, то один из его углов равен 30°

Answer 1

шта за задача?
это такое правило же
ну лан
она применима обычно для прямоугольных треугольников
один из углов равен 90 , другой 30 , следовательно последний равен 60
одни дополняют друг друга до 90 градусов
потом отношение противолежащего катета к гипотенузе - синус острого угла
sin30 = 0.5(1/2)
свойство есть что катет противолежащий углу в 30 градусов равен половине гипотенузы
с/sin90=a/sin30; 
c*sin30=a*sin90; 
c*1/2=a*1; 
a=1/2c.
или так !

Answer 2

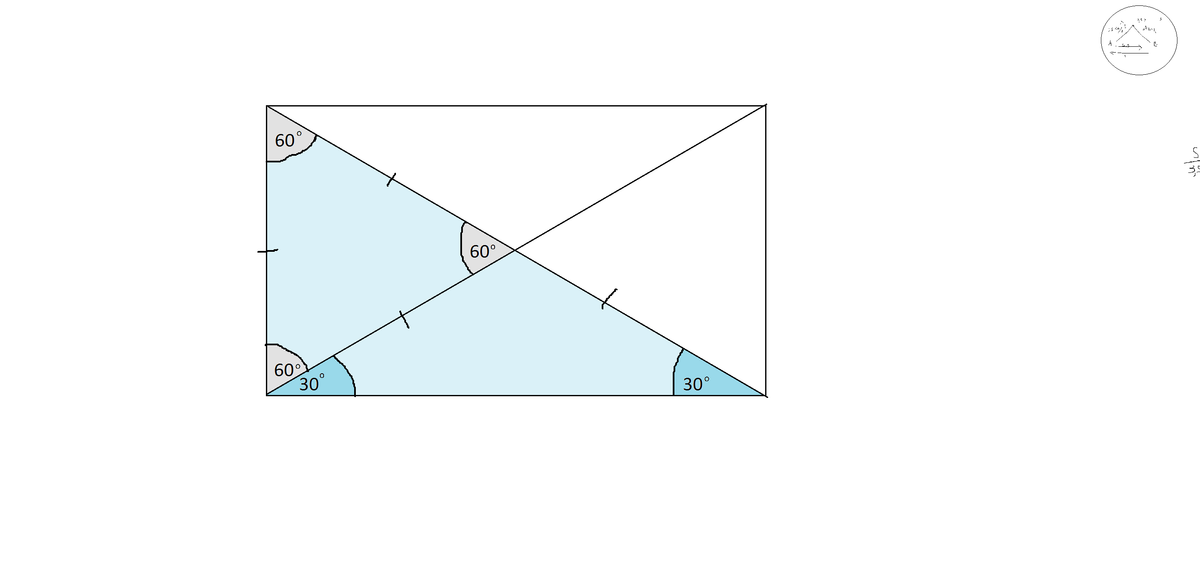
 Достроим этот треугольник до прямоугольника.  
Гипотенуза треугольника в  нем - диагональ. 
Соединим диагональю остальные два прямых угла. 
В прямоугольнике диагонали равны и точкой  пересечения  делятся пополам. 
 По условию меньший катет  данного в условии треугольника  равен половине гипотенузы.  
Следовательно, меньшая сторона  прямоугольника равна   половине  диагонали и образует с двумя половинами диагоналей  равносторонний  треугольник.  
В равностороннем треугольнике углы равны по 60°.   Отсюда второй угол, получившийся между диагональю и   большей стороной  при вершине прямоугольника, равен  90°-60°=30°  градусов.