Предмет: Геометрия,
автор: seoww
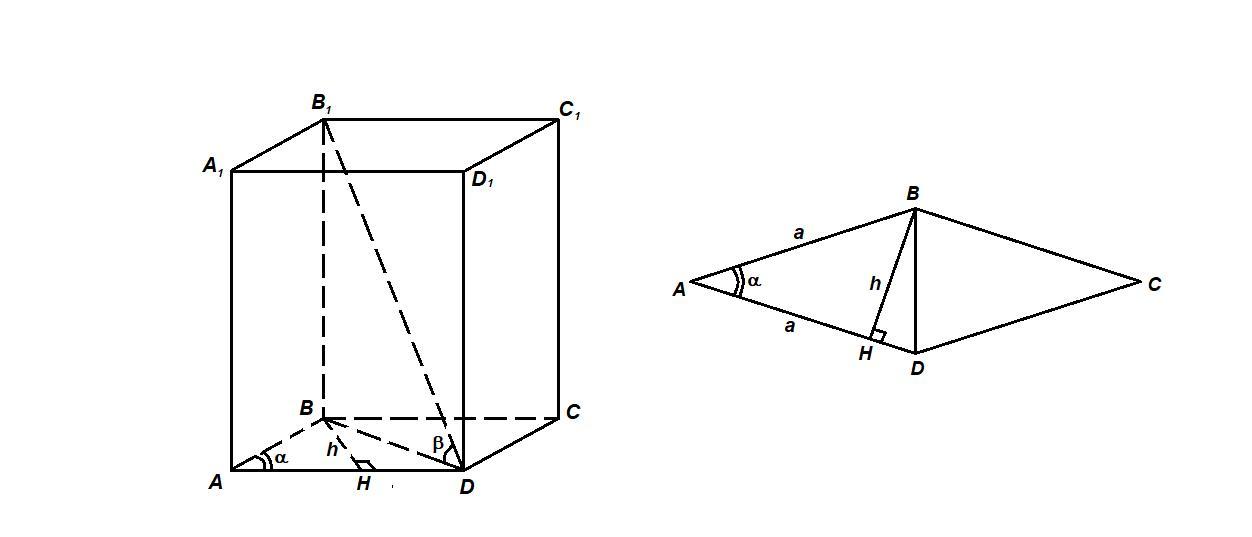
Основание прямой призмы - ромб с высотой h и острым углом α. Меньшая диагональ призмы наклонена к плоскости основания под углом β. Найдите объем призмы.
Ответы
Автор ответа:
1
Ответ:
Объяснение:
Из прямоугольного треугольника АВН:
Из треугольника ABD по теореме косинусов:
Из прямоугольного треугольника ВВ₁D:
Площадь основания:
Объем:
Приложения:
Похожие вопросы
Предмет: Қазақ тiлi,
автор: катя1162
Предмет: Русский язык,
автор: alena0719
Предмет: Английский язык,
автор: djukarevanatash
Предмет: Математика,
автор: dfgdfgdfgwetujh