Предмет: Алгебра,
автор: Аноним
Помогите с алгеброй!
Номер 6.11 б; 6.12 б; 6.13 б
Приложения:

Ответы
Автор ответа:
0
Решение:
Смотри вложение:...
Смотри вложение:...
Приложения:
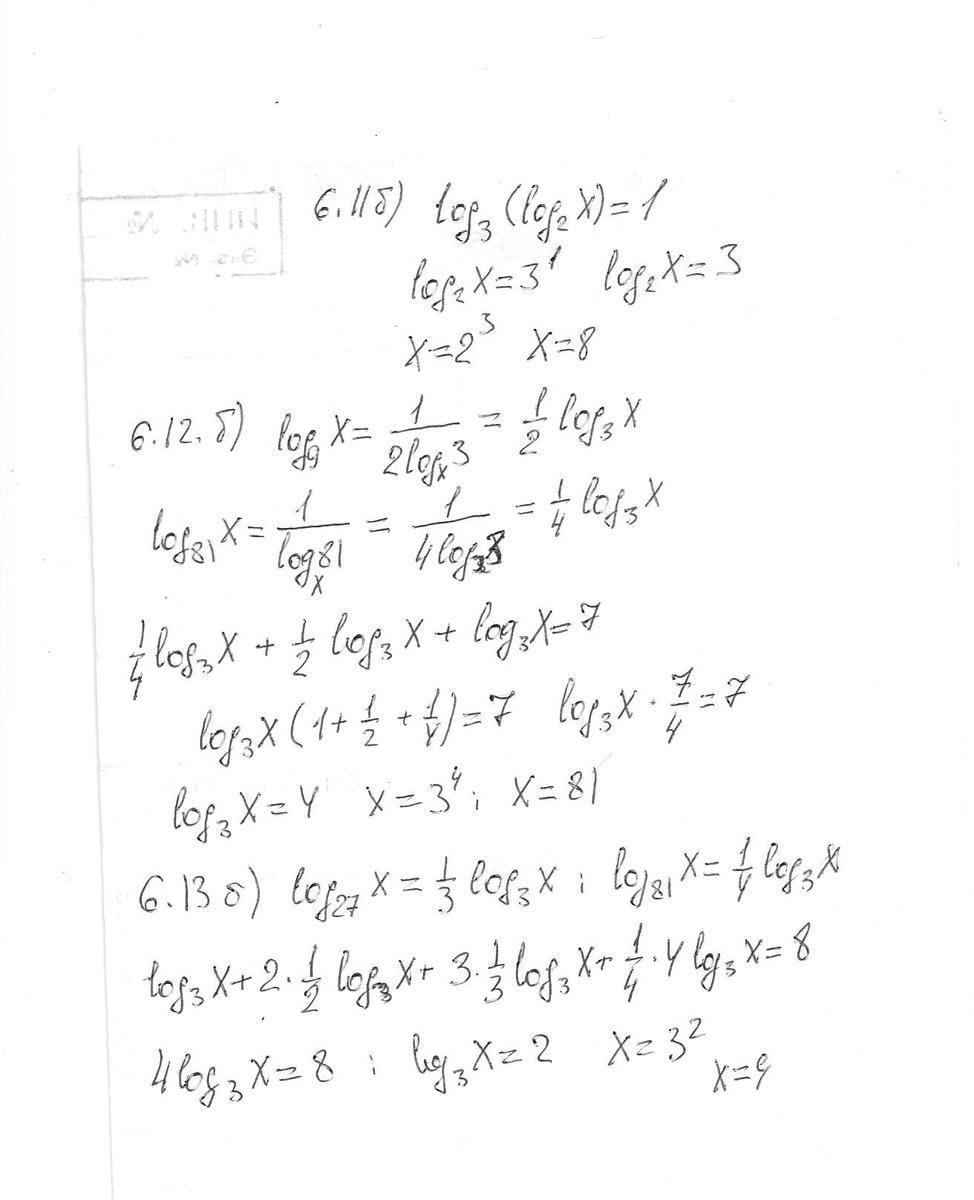
Автор ответа:
0
а можно более подробно?
Автор ответа:
0
6.11 б)
log3 (log2 x)=1
log3 (log2 x)=log3 3
log2x=3
log2 x=log2 8
x=8
6.12 б
log81 x+log9 x+log3 x=7
Log3 x/log3 81 + log3 x/log3 9 + log3 x = 7
log3 x/4 + log3 x/2 + log3 x = 7
log (3)x + 2*log(3)x + 4*log(3)x = 28
7 log(3)x = 28
divide by 7
log(3)x = 4
3^4 = x
x= 81
6.13 б
log3 x+2log9 x+3log 27x+4log81x=8
log[3]x+log[9]x^(2)+log[27]x^(3)+log[81]x^(4)=8
log[3]x+log[3^2]x^(2)+log[3^3]x^(3)+log[3^4]x^(4)=8
log[3]x+(2/2)log[3]x+(3/3)log[3]x+(4/4)log[3]x = 8
log[3]x + log[3]x + log[3]x+log[3]x = 8
4 log[3]x = 8
log[3]x = 2
x = 3^2
x = 9
log3 (log2 x)=1
log3 (log2 x)=log3 3
log2x=3
log2 x=log2 8
x=8
6.12 б
log81 x+log9 x+log3 x=7
Log3 x/log3 81 + log3 x/log3 9 + log3 x = 7
log3 x/4 + log3 x/2 + log3 x = 7
log (3)x + 2*log(3)x + 4*log(3)x = 28
7 log(3)x = 28
divide by 7
log(3)x = 4
3^4 = x
x= 81
6.13 б
log3 x+2log9 x+3log 27x+4log81x=8
log[3]x+log[9]x^(2)+log[27]x^(3)+log[81]x^(4)=8
log[3]x+log[3^2]x^(2)+log[3^3]x^(3)+log[3^4]x^(4)=8
log[3]x+(2/2)log[3]x+(3/3)log[3]x+(4/4)log[3]x = 8
log[3]x + log[3]x + log[3]x+log[3]x = 8
4 log[3]x = 8
log[3]x = 2
x = 3^2
x = 9
Приложения:
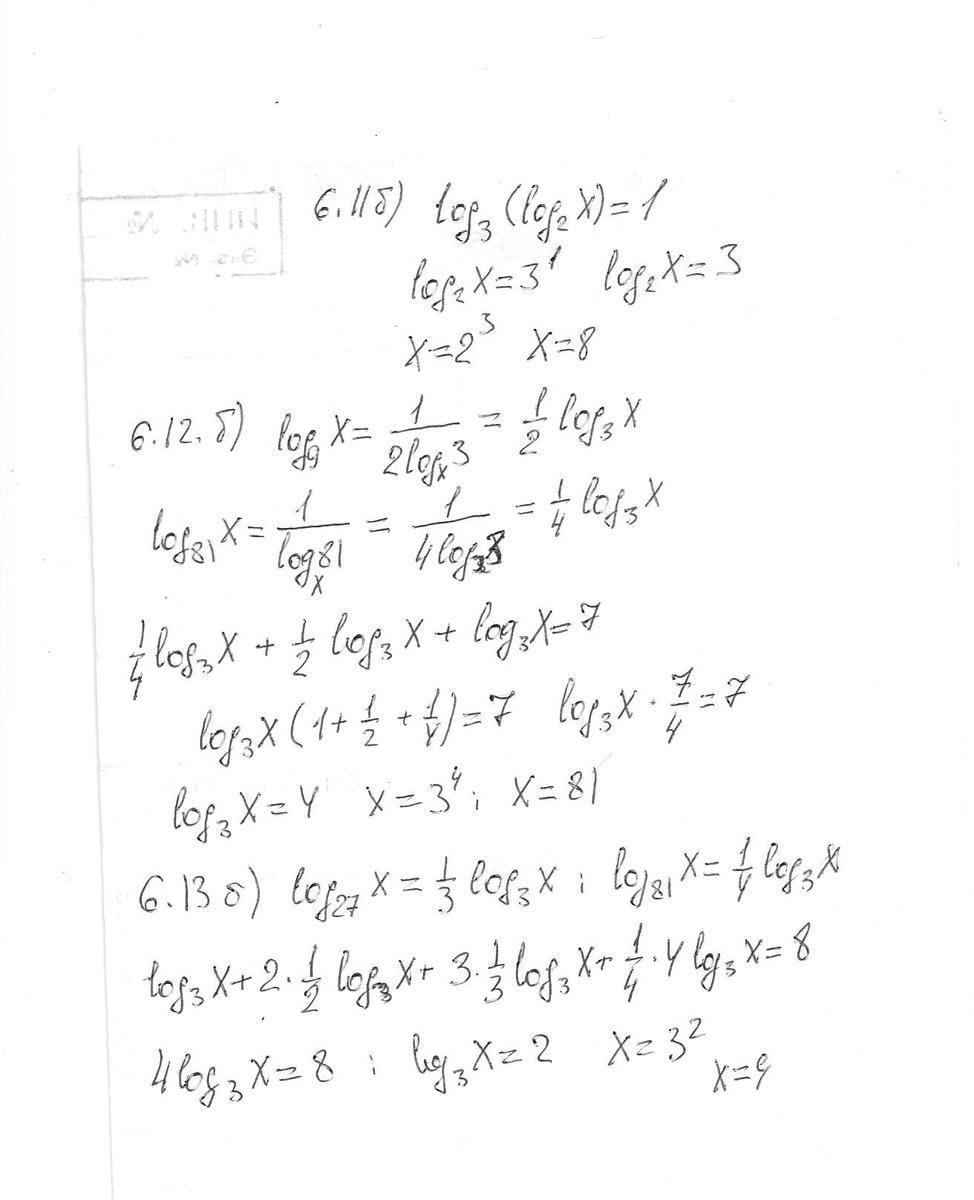
Похожие вопросы
Предмет: История,
автор: nastagruhina
Предмет: Русский язык,
автор: tyga112009
Предмет: Обществознание,
автор: tisc2005
Предмет: Математика,
автор: томарита